Lecture Hall

TG:

This is 26-100, one of the larger and more famous lecture halls at MIT. Right now Professor Walter Lewin is giving a lecture in 8.01, one of the most elementary courses offered at MIT. Now if you'll all be quiet, we'll take a look inside.

(opens door, WL is standing in front of a "board", probably a pad with pages he can fold to reveal different parts of the problem. He'll need to be able to point with something too.)

WL:

(gesturing at first page of stuff...nonsense equations) So you see, that is why you need to fully understand the theory of quantum gravity in order to complete this week's problem set.

WL:

But now let's review Newtonian mechanics by solving a simple problem, shall we? (pulls back sheet Words should probably be written out also)

A mass 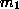suspended from a massless length 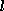string
Is released from angle 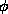and at the bottom of its swing
Well then it collides elastically with on a spring.
What is the amplitude?
Concern yourself with just the first collision for this test
Assuming the spring constant to be is prob'ly best
And that friction's not important and it all starts out at rest
Please find the amplitude?

T1:

That looks like a really tough problem!

T2:

At least it rhymes.

WL:

Has anyone solved the problem?

[silence]

WL:

Oh, come on, it's intuitively obvious!

[more silence]

WL:

It's trivial!

[still more silence]

WL:

Oh, well, I guess I'll present the solution.

The starting state consists of just potential energy
which is given by the formula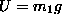
times the height (that's 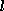times quantity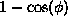
and now we can expect
that the swinging transfers energy that's stored inside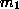
and it all becomes kinetic by the time the swing is done
so 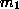has got momentum and the other mass has none
before the two connect
The bounce conserves kinetic energy and momentum
Thus the ratio of 's energy to 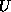becomes
four times the masses' product over the square of their sum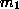
we now exclude.
So now the spring-mass system just begins to oscillate
there's no loss so max kinetic and potential thus equate
Potential's 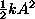in the most deflected state
where 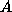is amplitude
Now take 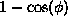times ,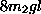
put the whole thing over , take the square root of this as well
times 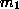over 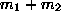now you can tell
we've found the amplitude

T1:

Wow. Did you understand that?

T2:

I think so...maybe MIT isn't that tough after all.

WL:

Well, enough of the easy stuff. Back to superstring theory. Did everyone bring in their neutrino-detectors?

(TG closes the door before even more esoteric stuff can be presented)

TG:

Ummm...We'd best be on our way now. We're walking ...we're walking.