skip to content

Research > Nonlinear Dynamics

Dynamical systems theory provides a wealth of mathematical tools and geometrical concepts for explaining complex real-world phenomena. We utilize these in the investigation of fundamental fluid flow phenomena in laboratory experiments. In the past, we have demonstrated that low-dimensional models can explain the behavior of highly-complex flows of a liquid crystal. More recently, the latest concepts regarding Lagrangian Coherent Structures have provided insight into the structure of turbulent fluid flow, the nature of unsteady flow separation and helped uncover internal wave attractors.

Funding for our research on Nonlinear Dynamics is provided by the MIT Ferry Fund, the ONR and the NSF.

Spotlight

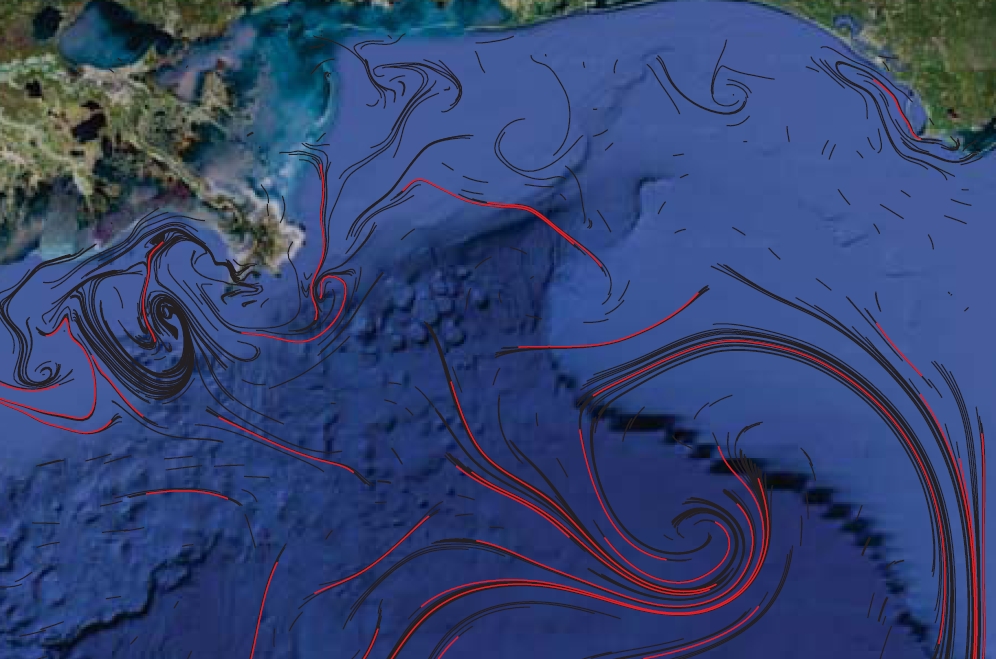
Lagrangian based methods for coherent structure detection

Understanding the transport of oil and debris is vital to environmental protection. By looking at the local deformation of the flow field, LCSs make it possible to identify the dominate structures that shape the overall flow and yield predictions on the movement of such contaminants. There has been a proliferation in the development of Lagrangian analytical methods for detecting coherent structures in fluid flow transport, yielding a variety of qualitatively different approaches. We have reviewed four approaches and demonstrated the utility of these methods.

A detailed report of this study has been published in Chaos: An Interdisciplinary Journal of Nonlinear Science [read the paper].
Through a review of past works, this article in Physics Today demonstrates the basis of LCSs and its future potential: [read the paper].

Relevant Publications

  1. Mullin, T. and Peacock, T., "Hydrodynamic instabilities in nematic liquid crystals under oscillatory shear," Proceedings of the Royal Society of London A, 455, 2635-2653 (1999). [link]
  2. Peacock, T., Mullin, T. and Binks, D.J., "Bifurcation phenomena in flows in a nematic liquid crystal," International Journal of Bifurcations and Chaos, 9, 427-441 (1999). [link]
  3. Peacock, T., Binks, D.J. and Mullin, T., "From low- to high-dimensional dynamics in a microscopic fluid flow," Physical Review Letters, 82, 1446-1449 (1999). [link]
  4. Peacock, T. and Mullin, T., "Homoclinic bifurcations in a liquid crystal flow," Journal of Fluid Mechanics, 432, 369-386 (2000). [link]
  5. Peacock, T. and Mullin T., "The transition to turbulence in a microscopic fluid flow," Physics of Fluids, 12, S8 (2000). [link]
  6. Mathur, M., Haller, G., Peacock, T., Ruppert-Felsot, J.E. and Swinney, H.L., "Uncovering the lagrangian skeleton of turbulence," Physical Review Letters, 98 (14), Art. No. 144502 (2007). [link]
  7. Peacock, T. and Bradley, E., "Going with (or against) the flow," Science, 320 (5881), 1302-1303 (2008). [link]
  8. Weldon, M., Peacock, T., Jacobs, G.B., Helu, M. and Haller, G., "Experimental and numerical investigation of the kinematic theory of unsteady separation," Journal of Fluid Mechanics, 611, 1-11 (2008). [link]
  9. Tang, W.E. and Peacock, T., "Lagrangian coherent structures and internal tide attractors," CHAOS, 20, 017508 (2010). [link]
  10. Peacock, T. and Dabiri, J., "Introduction to Focus Issue: Lagrangian coherent structures," CHAOS, 20, 017501 (2010). [link]
  11. Peacock, T. and Haller, G., "Lagrangian Coherent Structures: the hidden skeleton of fluid flows", Physics Today, 66, 41 (2013). [link]
  12. Allshouse, M.R. and Peacock, T., "Lagrangian based methods for coherent structure detection", CHAOS, 25, 097617 (2015). [link]
  13. Peacock, T., Froyland, G. and Haller, G., "Introduction to Focus Issue: Objective Detection of Coherent Structures", CHAOS, 25, 087201 (2015). [link]
  14. Allshouse, M.R. and Peacock, T., "Refining finite-time Lyapunov exponent ridges and the challenges of classifying them", CHAOS, 25(8), 087410 (2015). [link]
  15. Allshouse M. R., Ivey G. N., Xu J., Beegle-Krause C. J., Lowe R. J., Jones N. L. and Peacock T., “The impact of wind on the Lagrangian structure of ocean surface transport,” submitted.

People

back to top