Next: Steady State Laminar Boundary Up: No Title Previous: Introduction.

Boundary Layer Governing Equations.

In developing a mathematical theory of boundary layers, the first step is to show the existence, as the Reynolds number R tends to infinity, or the kinematic viscosity 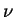$\nu$ tends to zero, of a limiting form of the equations of motion, different from that obtained by putting 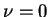$\nu = 0$ in the first place. A solution of these limiting equations may then reasonably be expected to describe approximately the flow in a laminar boundary layer for which R is large but not infinite. This is the basis of the classical theory of laminar boundary layers.

The full equation of motion for for a two-dimensional flow are:

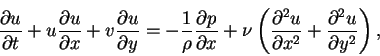$\begin{displaymath}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+... ...}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}}\right), \end{displaymath}$

(1)

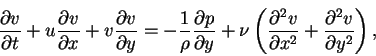$\begin{displaymath}\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+... ...}{\partial x^{2}}+\frac{\partial^{2}v}{\partial y^{2}}\right), \end{displaymath}$

(2)

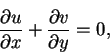$\begin{displaymath}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} = 0, \end{displaymath}$

(3)

where the x and y variables are, respectively, the horizontal and vertical coordinates, u and v are, respectively, the horizontal and vertical fluid velocities and p is the fluid pressure. A wall is located in the plane y = 0. We consider non-dimensional variables

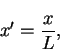$\begin{displaymath}x' = \frac{x}{L}, \end{displaymath}$

(4)

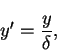$\begin{displaymath}y' = \frac{y}{\delta}, \end{displaymath}$

(5)

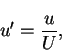$\begin{displaymath}u' = \frac{u}{U}, \end{displaymath}$

(6)

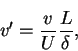$\begin{displaymath}v' = \frac{v}{U}\frac{L}{\delta}, \end{displaymath}$

(7)

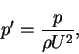$\begin{displaymath}p' = \frac{p}{\rho U^{2}}, \end{displaymath}$

(8)

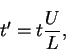$\begin{displaymath}t' = t\frac{U}{L}, \end{displaymath}$

(9)

where L is the horizontal length scale, 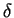$\delta$ is the boundary layer thickness at x = L, which is unknown. We will obtain an estimate for it in terms of the Reynolds number R. U is the flow velocity, which is aligned in the x-direction parallel to the solid boundary. The non-dimensional form of the governing equations is:

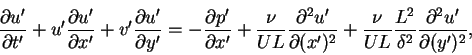$\begin{displaymath}\frac{\partial u'}{\partial t'}+u'\frac{\partial u'}{\partial... ...ac{L^{2}}{\delta^{2}}\frac{\partial^{2}u'}{\partial (y')^{2}}, \end{displaymath}$

(10)

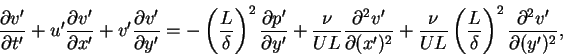$\begin{displaymath}\frac{\partial v'}{\partial t'}+u'\frac{\partial v'}{\partial... ...L}{\delta}\right)^{2}\frac{\partial^{2}v'}{\partial (y')^{2}}, \end{displaymath}$

(11)

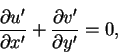$\begin{displaymath}\frac{\partial u'}{\partial x'}+\frac{\partial v'}{\partial y'} = 0, \end{displaymath}$

(12)

where the Reynolds number for this problem is

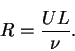$\begin{displaymath}R = \frac{UL}{\nu}. \end{displaymath}$

(13)

Inside the boundary layer, viscous forces balance inertia and pressure gradient forces. In other words, inertia and viscous forces are of the same order, so

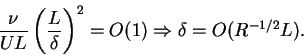$\begin{displaymath}\frac{\nu}{UL}\left(\frac{L}{\delta}\right)^{2} = O(1) \Rightarrow \delta = O(R^{-1/2}L). \end{displaymath}$

(14)

Now we drop the primes from the non-dimensional governing equations and with equation (2.14) we have

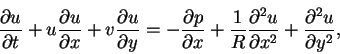$\begin{displaymath}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+... ...al^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}}, \end{displaymath}$

(15)

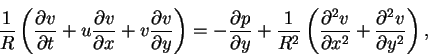$\begin{displaymath}\frac{1}{R}\left(\frac{\partial v}{\partial t}+u\frac{\partia... ...}{\partial x^{2}}+\frac{\partial^{2}v}{\partial y^{2}}\right), \end{displaymath}$

(16)

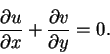$\begin{displaymath}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} = 0. \end{displaymath}$

(17)

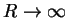In the limit $R \rightarrow \infty$ , the equations above reduce to:

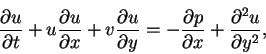$\begin{displaymath}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+... ...{\partial p}{\partial x}+\frac{\partial^{2}u}{\partial y^{2}}, \end{displaymath}$

(18)

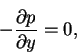$\begin{displaymath}-\frac{\partial p}{\partial y} = 0, \end{displaymath}$

(19)

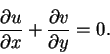$\begin{displaymath}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} = 0. \end{displaymath}$

(20)

Notice that according to equation (2.19), the pressure is constant across the boundary layer. In terms of dimensional variables, the system of equations above assume the form:

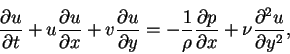$\begin{displaymath}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+... ...artial p}{\partial x}+\nu\frac{\partial^{2}u}{\partial y^{2}}, \end{displaymath}$

(21)

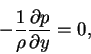$\begin{displaymath}-\frac{1}{\rho}\frac{\partial p}{\partial y} = 0, \end{displaymath}$

(22)

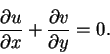$\begin{displaymath}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} = 0. \end{displaymath}$

(23)

To solve the system of equations above we need to specify initial and boundary conditions.

Next: Steady State Laminar Boundary Up: No Title Previous: Introduction.

Karl P Burr
2003-03-12