


Next: Similarity Solution.
Up: No Title
Previous: Boundary Layer Governing Equations.
We consider a flat plate at y=0 with a stream with constant speed U parallel to the plate. We are interested in the steady state solution. We are not interested in how the flow outside the boundary layer reached the speed U. In this case, we need only to consider boundary conditions and the equation (2.18) simplifies since
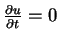 .
At the plate surface there is no flow across it, which implies that
.
At the plate surface there is no flow across it, which implies that
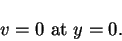 |
(24) |
Due to the viscosity we have the no slip condition at the plate. In other words,
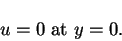 |
(25) |
At infinity (outside the boundary layer), away from the plate, we have that
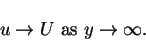 |
(26) |
For the flow along a flat plate parallel to the stream velocity U, we assume no pressure gradient, so the momentum equation in the x direction for steady motion in the boundary layer is
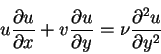 |
(27) |
and the appropriate boundary conditions are:
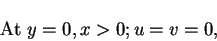 |
(28) |
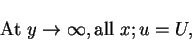 |
(29) |
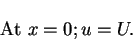 |
(30) |
These conditions demand an infinite gradient in speed at the leading edge x = y = 0, which implies a singularity in the mathematical solution there. However, the assumptions implicit in the boundary layer approximation break down for the region of slow flow around the leading edge. The solution given by the boundary layer approximation is not valid at the leading edge. It is valid downstream of the point x = 0. We would like to reduce the boundary layer equation (3.27) to an equation with a single dependent variable. We consider the stream function 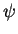 related to the velocities u and v according to the equations
related to the velocities u and v according to the equations
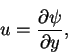 |
(31) |
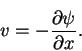 |
(32) |
If we substitute equations (3.31) and (3.32) into the equation (3.27), we obtain a partial differential equation for 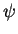 ,
which is given by
,
which is given by
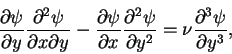 |
(33) |
and the boundary conditions (3.28) and (3.29) assume the form
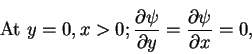 |
(34) |
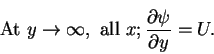 |
(35) |
The boundary value problem admits a similarity solution. We would like to reduce the partial differential equation (3.33) to an ordinary differential equation. We would like to find a change of variables which allows us to perform the reduction mentioned above.



Next: Similarity Solution.
Up: No Title
Previous: Boundary Layer Governing Equations.
Karl P Burr
2003-03-12
![]() .
At the plate surface there is no flow across it, which implies that
.
At the plate surface there is no flow across it, which implies that