


Next: Vorticity.
Up: Steady State Laminar Boundary
Previous: Steady State Laminar Boundary
We look for a one-parameter transformation of variables y, x and 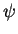 under which the equations for the boundary value problem for
under which the equations for the boundary value problem for 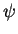 are invariant. A particularly useful transformation is
are invariant. A particularly useful transformation is
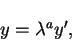 |
(36) |
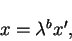 |
(37) |
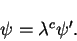 |
(38) |
Requiring the invariance of the equation (3.33) with respect to the transformation (3.36) to (3.38) gives
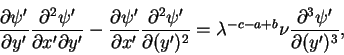 |
(39) |
and performing the same for the boundary conditions gives
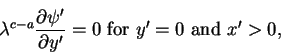 |
(40) |
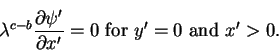 |
(41) |
The requirement of invariance in the equations (3.39) to (3.41) leads to the algebraic relations
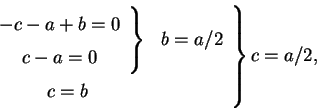 |
(42) |
which suggest that we take the change of variables
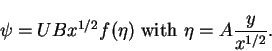 |
(43) |
If we substitute the change of variables above into equation (3.33), we obtain an ordinary differential equation for 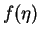 ,
given by
,
given by
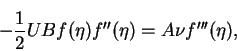 |
(44) |
and we chose
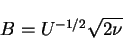 |
(45) |
so that
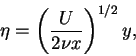 |
(46) |
such that
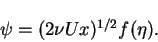 |
(47) |
The change of variables given by equations (3.46) and (3.47) is analog to the change of variables used in the Rayleigh problem discussed in Capter 1, where instead of x/U we have time t. The analogy is that the disturbance due to the plate spreads out into the stream at the rate given by the unsteady problem (Rayleigh problem), but at the same time it is swept downstream with the fluid. The Rayleigh problem in Chapter 1 can be used to give an approximate solution to the problem here. The expression for the flow velocity u for the Rayleigh problem can be used to estimate the downstream velocity relative to the plate by identifying t with x/U. This is equivalent to the following approximations in the momentum equation
Firstly, the convection terms on the left are replaced by the approximation
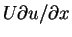 ,
and, secondly, the term
,
and, secondly, the term
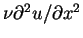 is neglected in the viscous terms on the right. In this way, we obtain the diffusion equation for u with t replaced by x/U. The boundary layer approximation retains the convection terms in full and makes only the second simplification. The Rayleigh approximation obviously overestimates the convection effects; hence its prediction of the boundary layer thickness will be too small and the value of the shear stress to great.
is neglected in the viscous terms on the right. In this way, we obtain the diffusion equation for u with t replaced by x/U. The boundary layer approximation retains the convection terms in full and makes only the second simplification. The Rayleigh approximation obviously overestimates the convection effects; hence its prediction of the boundary layer thickness will be too small and the value of the shear stress to great.
The equation that 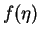 has to satisfy is
has to satisfy is
with boundary conditions:
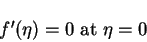 |
(49) |
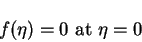 |
(50) |
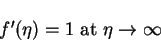 |
(51) |
This is a boundary value problem for the function 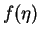 which has no closed form solution, so we need to solve it numerically. Solving boundary value problems numerically is not an easy task. We would like to reduce this boundary value problem to an initial value problem. For the equation (3.48) this is possible. If
which has no closed form solution, so we need to solve it numerically. Solving boundary value problems numerically is not an easy task. We would like to reduce this boundary value problem to an initial value problem. For the equation (3.48) this is possible. If 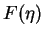 is any solution of equation (3.48), also
is any solution of equation (3.48), also
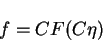 |
(52) |
is a solution, with C an arbitrary constant of homology. Then,
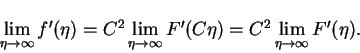 |
(53) |
Since
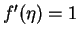 for
for
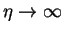 ,
we have that
,
we have that
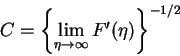 |
(54) |
We know from equation (3.52) that
f''(0) = C3F''(0), and if we specify
F''(0) = 1, we have from equation (3.54) that
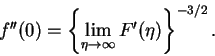 |
(55) |
To obtain the value f''(0), we need to evaluate numerically the initial value problem for 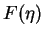 ,
given by equation (3.48) with initial conditions
F(0) = F'(0) = 0 and F''(0)=1, for a large value of
,
given by equation (3.48) with initial conditions
F(0) = F'(0) = 0 and F''(0)=1, for a large value of 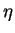 to obtain
to obtain 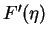 as
as
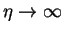 and f''(0) (see equation (3.55). Therefore, the initial value problem for
and f''(0) (see equation (3.55). Therefore, the initial value problem for 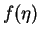 equivalent to the boundary value problem given by equations (3.48) to (3.51) is given by the ordinary differential equation (3.48) plus the initial conditions
equivalent to the boundary value problem given by equations (3.48) to (3.51) is given by the ordinary differential equation (3.48) plus the initial conditions
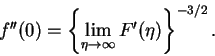 |
(58) |
Below we illustrate the result of the numerical integration of the initial value problem given by equation (3.48) and initial conditions (3.56) to (3.58) in the figures 1. We obtained numerically that
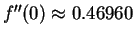 .
.
Figure:
Functions
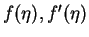 and
and 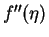 .
The horizontal axis represents the range of values of
.
The horizontal axis represents the range of values of 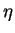 considered, and in the vertical axis we have the values of the functions
considered, and in the vertical axis we have the values of the functions
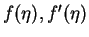 and
and 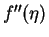 .
.
|
|
Once we have computed numerically 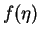 and its derivatives up to second order, we can obtain the velocity components (u,v) at any point (x,y) of the flow domain, according to the equations
and its derivatives up to second order, we can obtain the velocity components (u,v) at any point (x,y) of the flow domain, according to the equations
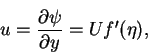 |
(59) |
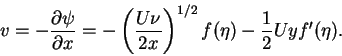 |
(60) |



Next: Vorticity.
Up: Steady State Laminar Boundary
Previous: Steady State Laminar Boundary
Karl P Burr
2003-03-12
![]() under which the equations for the boundary value problem for
under which the equations for the boundary value problem for ![]() are invariant. A particularly useful transformation is
are invariant. A particularly useful transformation is
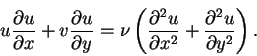
![]() has to satisfy is
has to satisfy is
![\includegraphics[width=5.5in,height=5.5in]{ps/func_ff1f2.eps}](img73.gif)
![]() and its derivatives up to second order, we can obtain the velocity components (u,v) at any point (x,y) of the flow domain, according to the equations
and its derivatives up to second order, we can obtain the velocity components (u,v) at any point (x,y) of the flow domain, according to the equations