


Next: Stress.
Up: Similarity Solution.
Previous: Similarity Solution.
The vorticity of the flow in Cartesian coordinates in term of dimensional variables is given by
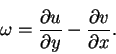 |
(61) |
If we non-dimensionalize the vorticity, according to
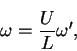 |
(62) |
the non-dimensional form of the equation (3.61) is
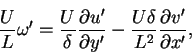 |
(63) |
and since
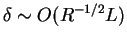 ,
we have that
,
we have that
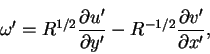 |
(64) |
and in the limit
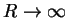 we have
we have
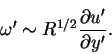 |
(65) |
In the context of the boundary-layer approximation, the vorticity in terms of dimensional variables is given by
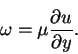 |
(66) |
We can write the vorticity for the Blasius boundary layer similarity solution by placing equation (3.47) for 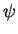 into the equation (3.66), which gives
into the equation (3.66), which gives
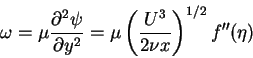 |
(67) |



Next: Stress.
Up: Similarity Solution.
Previous: Similarity Solution.
Karl P Burr
2003-03-12
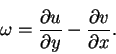
![]() into the equation (3.66), which gives
into the equation (3.66), which gives