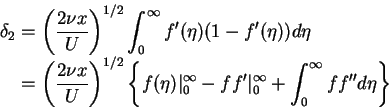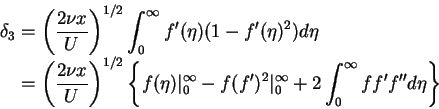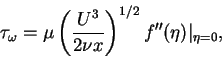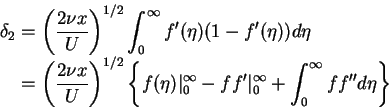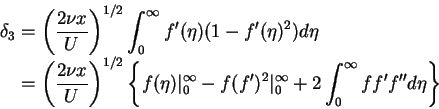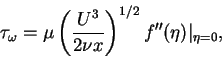Quantities for the Blasius Boundary Layer Solution.

Next: Momentum and Energy Equations. Up: Boundary-layer Thickness, Skin friction, Previous: Boundary-layer Thickness, Skin friction,

Quantities for the Blasius Boundary Layer Solution.

For the Blasius similarity solution for a two-dimensional boundary layer given by equation (3.47), we can compute the the quantities defined above:

Displacement thickness $\delta_{1}$ :

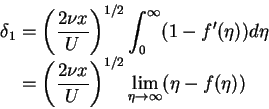$\begin{displaymath}\begin{split} \delta_{1} & = \left(\frac{2\nu x}{U}\right)^{1... ...)^{1/2}\lim_{\eta \rightarrow \infty}(\eta-f(\eta)) \end{split}\end{displaymath}$ (84)
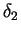Momentum thickness $\delta_{2}$ :

$\begin{displaymath}\begin{split} \delta_{2} & = \left(\frac{2\nu x}{U}\right)^{1... ...nfty}_{0}+\int_{0}^{\infty}ff''d\eta\right\} \end{split}\notag \end{displaymath}$

and taking into account the boundary conditions (3.49) to (3.51), we obtain that

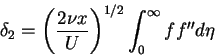$\begin{displaymath}\delta_{2} = \left(\frac{2\nu x}{U}\right)^{1/2}\int_{0}^{\infty}ff''d\eta \end{displaymath}$ (85)
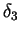Energy thickness $\delta_{3}$ :

$\begin{displaymath}\begin{split} \delta_{3} & = \left(\frac{2\nu x}{U}\right)^{1... ...}_{0}+2\int_{0}^{\infty}ff'f''d\eta\right\} \end{split} \notag \end{displaymath}$

and taking into account the boundary conditions (3.49) to (3.51), we obtain that

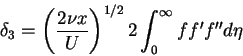$\begin{displaymath}\delta_{3} = \left(\frac{2\nu x}{U}\right)^{1/2}2\int_{0}^{\infty}ff'f''d\eta \end{displaymath}$ (86)
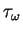Skin friction $\tau_{\omega}$ :

$\begin{displaymath}\tau_{\omega} = \mu\left(\frac{U^{3}}{2\nu x}\right)^{1/2}f''(\eta)\vert _{\eta = 0}, \notag \end{displaymath}$

and according to the initial condition f''(0) = 1, we have that

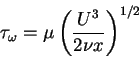$\begin{displaymath}\tau_{\omega} = \mu\left(\frac{U^{3}}{2\nu x}\right)^{1/2} \end{displaymath}$ (87)
Dissipation integral D:

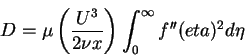$\begin{displaymath}D = \mu\left(\frac{U^{3}}{2\nu x}\right)\int_{0}^{\infty}f''(eta)^{2}d\eta \end{displaymath}$ (88)

Next: Momentum and Energy Equations. Up: Boundary-layer Thickness, Skin friction, Previous: Boundary-layer Thickness, Skin friction,

Karl P Burr
2003-03-12