


Next: Quantities for the Blasius
Up: No Title
Previous: Stress.
According to equation (2.22), the pressure across the boundary layer is constant in the boundary-layer approximation, and its value at any point is therefore determined by the corresponding main-stream conditions. If U(x,t) now denotes the main stream velocity, so that
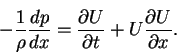 |
(76) |
Elimination of the pressure from equation (2.21) gives in terms of dimensional variables the boundary layer momentum equation
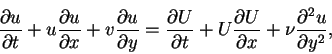 |
(77) |
and from equation (2.23), we have the mass conservation equation
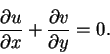 |
(78) |
In most physical problems the solutions of the boundary layer equations (4.77) and (4.78) are such that the velocity component u attains its main-stream value U only asymptotically as
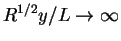 .
The thickness of the layer is therefore indefinite, as there is always some departure from the asymptotic value at any finite distance y from the surface. In practice the approach to the limit is rapid and a point is soon reached beyond which the influence of viscosity is imperceptible. It would therefore be possible to regard the boundary layer thickness as a distance
.
The thickness of the layer is therefore indefinite, as there is always some departure from the asymptotic value at any finite distance y from the surface. In practice the approach to the limit is rapid and a point is soon reached beyond which the influence of viscosity is imperceptible. It would therefore be possible to regard the boundary layer thickness as a distance 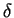 from the surface beyond which
u/Y > 0.99, for example, but this is not sufficiently precise (since
from the surface beyond which
u/Y > 0.99, for example, but this is not sufficiently precise (since
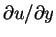 is small there) for experimental work, and is not of theoretical significance.
is small there) for experimental work, and is not of theoretical significance.
The scale of the boundary layer thickness can, however, be specified adequately by certain lengths capable of precise definition, both for experimental measurement and for theoretical study. These measures of boundary layer thickness are defined as follows:
- Displacement thickness
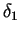 :
:
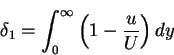 |
(79) |
- Momentum thickness
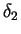 :
:
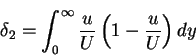 |
(80) |
- Energy thickness
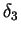 :
:
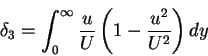 |
(81) |
The upper limit of integration is taken as infinity owing to the asymptotic approach of u/U to 1, but in practice the upper limit is the point beyond which the integrand is negligible.
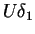 is the diminution, due to the boundary layer, of the volume flux across a normal to the surface; the streamlines of the outer flow are thus displaced away from the surface through a distance
is the diminution, due to the boundary layer, of the volume flux across a normal to the surface; the streamlines of the outer flow are thus displaced away from the surface through a distance
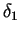 .
Similarly,
.
Similarly,
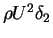 is the flux of the defect of momentum, and
is the flux of the defect of momentum, and
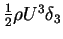 is the flux of defect of kinetic energy.
is the flux of defect of kinetic energy.
Two other quantities related to these boundary layer thickness are the skin friction
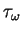 and the dissipation integral D. The skin friction is defined as the shearing stress exerted by the fluid on the surface over which it flows, and is therefore the value of
and the dissipation integral D. The skin friction is defined as the shearing stress exerted by the fluid on the surface over which it flows, and is therefore the value of 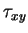 at y = 0, which by (3.74) is
at y = 0, which by (3.74) is
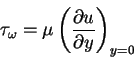 |
(82) |
in terms of dimensional variables. The rate at which energy is dissipated by the action of viscosity has been shown to be
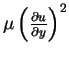 per unit time per unit volume, and D is the integral of this across the layer:
per unit time per unit volume, and D is the integral of this across the layer:
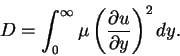 |
(83) |
Consequently, D is the total dissipation in a cylinder of small cross-section with axis normal to the layer per unit time per unit area of cross-section.



Next: Quantities for the Blasius
Up: No Title
Previous: Stress.
Karl P Burr
2003-03-12
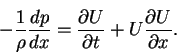
![]() is the diminution, due to the boundary layer, of the volume flux across a normal to the surface; the streamlines of the outer flow are thus displaced away from the surface through a distance
is the diminution, due to the boundary layer, of the volume flux across a normal to the surface; the streamlines of the outer flow are thus displaced away from the surface through a distance
![]() .
Similarly,
.
Similarly,
![]() is the flux of the defect of momentum, and
is the flux of the defect of momentum, and
![]() is the flux of defect of kinetic energy.
is the flux of defect of kinetic energy.
![]() and the dissipation integral D. The skin friction is defined as the shearing stress exerted by the fluid on the surface over which it flows, and is therefore the value of
and the dissipation integral D. The skin friction is defined as the shearing stress exerted by the fluid on the surface over which it flows, and is therefore the value of ![]() at y = 0, which by (3.74) is
at y = 0, which by (3.74) is
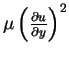 per unit time per unit volume, and D is the integral of this across the layer:
per unit time per unit volume, and D is the integral of this across the layer: