13.021 - Marine Hydrodynamics, Fall 2003 Lecture 7
Copyright © 2003 MIT - Department of Ocean Engineering, All rights reserved.

13.021 - Marine Hydrodynamics
Lecture 7

Chapter 3 - Ideal Fluid Flow

We define Ideal fluid as inviscid ($\nu = 0$) and incompressible ( $\frac{D\rho}{Dt} = 0$). The Reynolds number is defined as the ration between the inertial and viscous forces, so

$$R_e = \frac{\mbox{inertia}}{\mbox{viscous}} = \frac{UL}{\nu }.$$

For `typical' problems we are interested in (for example, $L \ges 1m, U \ge 1m/s$ and $\nu _{water} = 10^{ - 6}{m^2}/s$) we have that

$$\frac{\nu }{UL} = R_e^{ - 1} < < 1 ( \le 10^{ - 6}).$$

In other words, the viscous effect are much smaller than the inertial effects, and under certain circunstances (streamlined bodies), the viscous effects are restricted to a thin layer (boundary layer) around the boundaries of the flow (surfaces of streamlined bodies and their wake, for example). Therefore, outside this thin layer, ideal fluid is a good approximation. (Movie to illustrate the boundary layer along body surfaces and how its thickness depends on the Reynolds number)

Governing Equations

The governing equations (continuity and momentum equation) for the case of ideal flow assume the form:

• Continuity:
  
  $$\nabla \cdot \vec{v} = 0$$
  
  

• Momentum (Navier Stokes $\Rightarrow$ Euler equation):
  
  $$\frac{\partial\vec{v}}{\partial t} +\vec{v} \cdot \nabla \vec{v} = - \frac{1}{\rho }\nabla p - g\hat {j}$$
  
  
  By neglecting the viscous stress term ( $\nu\nabla^{2}\vec{v}$) in the Navier-Stokes equation, this reduces to the Euler equation. Navier-Stokes equation is a second order partial differential equation (2$^{nd}$ order in $\nabla ^{2}$), but Euler equation is a first order partial differential equation. This is a considerable mathematical simplification, and a wide variety of ideal flow problems are amenable to solution.
  

Boundary Conditions for Euler Equation (Ideal Flow).

• Kinematic Boundary Condition:
  
  $$\vec{v} \cdot \hat {n} = \underbrace {\vec{u} \cdot \hat {n}... ...mbox{known}} \quad \leftarrow \mbox{\lq\lq No Flux'' - free slip}$$
  
  
  Note: The "No slip" condition $\vec{v}\cdot\hat{t} = \vec{U}\cdot\hat{t}$ does not apply since the assumption of ideal fluid assume no viscous forces ($\nu = 0$).
  
• Dynamic Boundary Condition: specify the pressure ( $p = \ldots$) at the boundary. We cannot specify tangential stress $\tau_{ij}$ since the ideal fluid assumption implies in no viscous forces ($\nu = 0$).

Circulation

We use the greek letter $\Gamma$ to denote the Circulation of the flow (around a closed contour $C$).

We define the circulation $\Gamma$ around an arbitrary closed contour $C$ according to the contour integral

$$\Gamma = \int_C {\underbrace {\vec{v} \cdot d\vec{x}. }_{\b... ...ngential} } \\ \mbox{\tiny {velocity}} \\ \end{array}}}$$

illustrated in the figure above. According to the definition above, $\Gamma$ is obtained at a given instant (Eulerian idea). We take a ``snapshot'' of the flow, and compute $\Gamma$ according to the equation above. For a different instant, the snapshot of the flow may be different (unsteady flow, for example), so the value of $\Gamma$ for the same contour $C$ may be different.

Kelvin's Theorem (KT):

For ideal fluid under conservative body forces,

$$\frac{d\Gamma }{dt} = 0$$

for any material contour $C$, i.e., the value of the circulation $\Gamma$ remains constant. For a proof, please see JNN pp 103 (Mathematical Proof) . This is a statement of conservation of angular momentum.

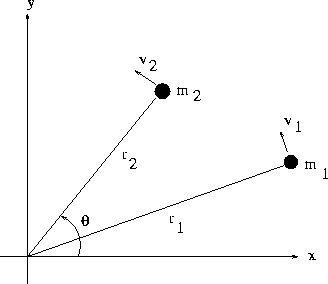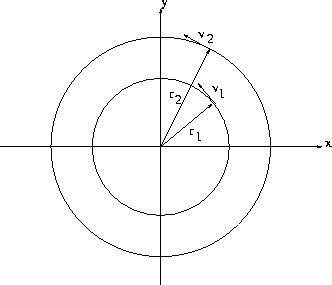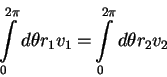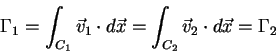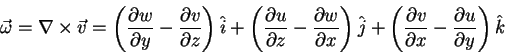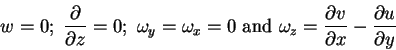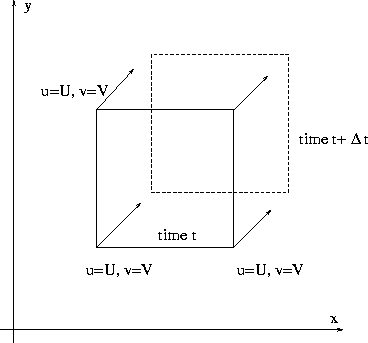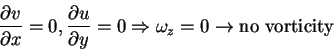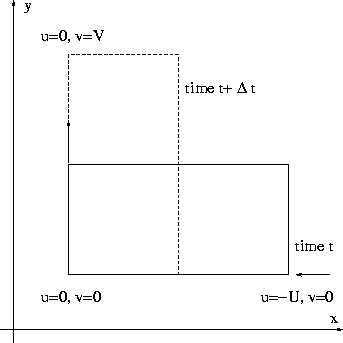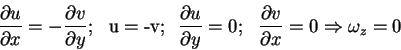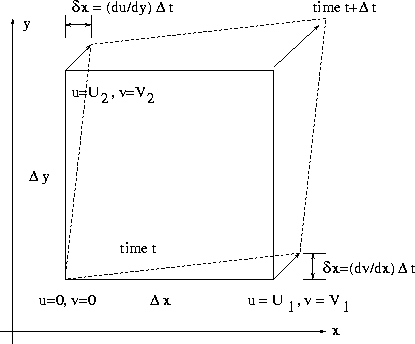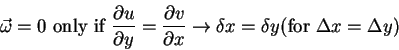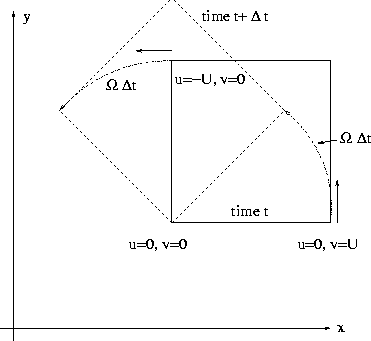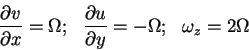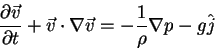
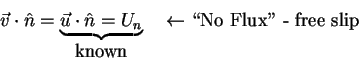
Kinematics of a small deformable body	For Ideal fluid under conservative body forces
1. Uniform translation $\rightarrow$ Linear Momentum	1. Can change
2. Rigid body rotation $\rightarrow$ Angular Momentum	2. By K.T., cannot change
3. Pure strain $\rightarrow$ no linear or angular	3. Can change
Momentum involved (No change in volume).
4. Volume dilatation	4. Not allowed (incompressible fluid)

For ideal fluid, Angular momentum is conserved.

1.

Angular Momentum $\times$ angular velocity $\vec{\omega }$.
For example:

Angular momentum:

$$\vec{L} = \vec{r}\times\vec{v} = mvr = mr^{2}\dot{\theta}$$

Conservation of angular momentum implies that:

$$m_{1}v_{1}r_{1} = m_{2}v_{2}r_{2},$$

but $m_{1} = m_{2} \Rightarrow v_{1}r_{1} = v_{2}r_{2}$.
Note: conservation of angular momentum does not imply constant angular velocity.

2.

A circular material contour $C_{m}$.

$$\int\limits_0^{2\pi } {d\theta r_1 v_1 = } \int\limits_0^{2\pi } {d\theta r_2 v_2 }$$

3.

For arbitrary material contour $C_{m}$

$$\Gamma _1 = \int_{C_1 }\vec{v}_1 \cdot d\vec{x} = \int_{C_2 }\vec{v}_2 \cdot d\vec{x} = \Gamma _2$$

Vorticity:

$$\vec{\omega} = \nabla \times \vec{v} = \left( {\frac{\partial... ...}{\partial x} - \frac{\partial u}{\partial y} \right)\hat {k}$$

Relationship between vorticity and circulation - Apply Stokes' Theorem:

$$\Gamma = \oint\limits_C \vec{v} \cdot d\vec{x} \underbrace{=}... ...a } \cdot \hat {n}dS = \mbox{\ Flux of vorticity out of\ } S$$

What is vorticity?

For example, consider the special case: For 2D flow,

$$w = 0;\ \frac{\partial }{\partial z} = 0;\ \omega _{y}=\omega... ...\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}$$

1.

Translation: $u =$ constant, $v =$ constant

$$\frac{\partial v}{\partial x} = 0,\frac{\partial u}{\partial y} = 0 \Rightarrow \omega _z = 0 \to \mbox{no vorticity}$$

2.

Pure Strain: (no change in volume)

$$\frac{\partial u}{\partial x} = - \frac{\partial v}{\partial ... ...\frac{\partial v}{\partial x} = 0 \Rightarrow \omega _z = 0$$

3.

Angular deformation

$$\vec{\omega} = 0 \mbox{\ only if\ } \frac{\partial u}{\partia... ...arrow \delta x = \delta y (\mbox{for\ } \Delta x = \Delta y)$$

4.

Pure Rotation

Pure rotation with angular velocity $\Omega$

$$\frac{\partial v}{\partial x} = \Omega ;\ \ \frac{\partial u}{\partial y} = - \Omega ;\ \ \omega _z = 2\Omega$$

i.e. vorticity $\propto$ 2(angular velocity).

For irrotational Flow:

$$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightha... ...ghtarrow \Gamma \equiv 0 \mbox{\ for any closed contour \ } C$$

Suppose that at $t=t_{o}$, the flow is irrotational, i.e. $\Gamma \equiv 0$ for all closed contours (material or not) $C$. Then for ideal fluid under conservative body forces, Kelvin's theorem states that $\Gamma \equiv 0$ for all closed material contours $C$ for all time $t$. i.e., once irrotational, always irrotational (Special case of Kelvin's theorem).