
| Vol.
XXI No.
4 March / April / May 2009 |
| contents |
| Printable Version |
MIT Poetry
On Becoming Housemasters
It never hurts to remind ourselves that MIT has the greatest students in the world, and that we have a profound obligation to give them an equally great MIT education. For the past few years, the MIT faculty has been engaged in a process of reevaluating the undergraduate program. The Mathematics faculty, a participant in this important process, is reviewing its own course offerings. Mathematics subjects are a central feature of the General Institute Requirements. It is time once again to revisit these basic but nontrivial questions: What mathematics should all MIT undergraduates learn? How best do we teach it to them?
The Mathematics Department is reexamining the core undergraduate mathematics subjects. The scope of this effort will include the basic freshman calculus GIR sequence 18.01 and 18.02 along with their variants. Additionally, we are rethinking 18.03 Differential Equations, 18.05 Probability and Statistics, and 18.06 Linear Algebra. This article serves to “get the word out” about this curriculum review. We welcome your input to: mathcore@mit.edu.
Here's the situation now in the freshman math subjects. Calculus I (18.01) covers single-variable calculus: differentiation, integration, applications to simple modeling, with very brief introductions to low-order Taylor approximations, some infinite integrals and their related series, and polar coordinates. Calculus II (18.02) is multivariable calculus: a brief introduction to vectors and matrices, then partial differentiation and multiple integration, gradient, divergence and curl, line and surface integrals, the divergence and Stokes theorems. Both of these subjects are taught in lecture/recitation format. One faculty member lectures for the entire semester, three times a week for an hour. A mix of mainly post-doctoral instructors and TAs handles the twice-weekly recitations.
We offer two additional placement options into the 18.01 – 18.02 sequence for students with sufficient preparation. About half the freshmen place out of 18.01 entirely and enter immediately into 18.02. Or, freshmen may partially place out of 18.01 by demonstrating that they have mastered the high school calculus AB syllabus – roughly half of the 18.01 material. With this head start they may take 18.01A – 18.02A which covers the remainder of 18.01 in six weeks and then continues with 18.02. This shortened sequence occupies the fall term and may be finished either over IAP or during the first half of the spring term, for a total of 1.5 semesters of instruction. Thus we provide three entry points into calculus to accommodate differing backgrounds.
In addition, we offer several alternate calculus “flavors” for students desiring a different point of view. Instead of 18.02, students may elect 18.022 to experience a more theoretical emphasis, or 18.023 to see more applications. Finally, instead of 18.01 – 18.02, mathophiles with some prior calculus background may choose the 18.014 – 18.024 sequence to get a proof-oriented, rigorous development of the subject.
Calculus Options |
|
| 18.01 - 18.02 | 2 terms, basic sequence |
| 18.01A - 18.02A | 1.5 terms, skips half of 18.01 |
| 18.02 Fall | 1 term, skips 18.01 |
| 18.022 Fall | 1 term, extra theory, skips 18.01 |
| 18.023 Fall | 1 term, extra applications, skips 18.01 |
| 18.014 - 18.024 | 2 terms, rigorous |
What might we accomplish with a revision of the curriculum? We’ve come up with several ways we might improve our current program. The ideas here are not necessarily optimal, and are certainly not intended to be an exhaustive list. We offer them mainly to get the conversation started.
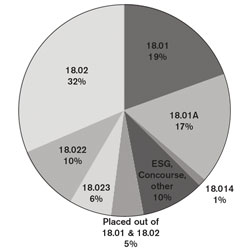
(click on image to enlarge)
As the accompanying pie chart shows, only about 19% of the freshman class selects the basic 18.01 – 18.02 sequence; the rest place out of 18.01 to varying degrees. Thus for most of our undergraduates, the de facto calculus course requirement ends up being less than two full subjects taken at MIT, because most students already know some calculus before they arrive here. Twenty years ago, over half of our entering students took 18.01. Today, calculus has moved into the high-school curriculum for many of our students. That shift frees up some of their time at MIT.
This shift may present an opportunity to utilize the freed-up time in more specific ways. Currently, students receive course credit for advanced placement, which allows them to use the freed-up time to take some other subject or simply to have more free time in their schedule. Proposal: We could change the math GIR to encompass only the 1.5 semesters of 18.01A – 18.02A plus one half-semester of something else, for example a shortened introduction to probability and statistics. A serious problem with this proposal is that the 200 or so freshmen who now take the full basic sequence would be at a disadvantage because they would need to complete the missing AB-syllabus half of 18.01 before they could start their math GIR. We could require all entering students to know enough calculus to begin with 18.01A, and ask them to take a preparatory summer class prior to entering if they don’t have this background, but that would place a big – probably too big – burden on certain students, and add significant complexity to the transition into MIT.
The absence of probability and statistics is a major gap in the present structure of the GIRs. Some knowledge of probability is simply indispensable these days in many disciplines and careers. An MIT education should provide that knowledge. Our post-graduation surveys of mathematics majors consistently show that our own graduates wish they had learned more probability and statistics.
We could introduce this material into the GIRs as mentioned above. Alternatively, we could substitute probability for some other material in the basic calculus sequence. The second half of 18.02 is devoted to vector integral calculus culminating in the divergence and Stokes theorems. Though that material fits naturally with multi-variable calculus and is useful in subjects like electricity and magnetism, thermodynamics, and fluid mechanics, the need for it may have diminished in recent years and therefore a more abbreviated treatment may be adequate. We’ve experimented with a few lectures on probability in 18.02 and 18.01A. Whether more probability and statistics can be added sensibly to 18.02 in place of some vector calculus requires further study.
Less radical adjustments in the curriculum are also under consideration. We have engaged with other departments to solicit suggestions about new topics and applications for inclusion in calculus and differential equations lectures and problem sets.
We encourage faculty from across the Institute to become involved in crafting the basic mathematics curriculum so that we can best serve our students by enhancing the breadth and relevance of these subjects.
In addition to suggestions as to content and problem material, we’d welcome an occasional guest lecture on an interesting application (preferably reinforced with a problem contributed to that week's pset!), or possibly some form of lecture or recitation co-teaching if there were interest and it seemed workable.
Several tempting ideas for improving our core math curriculum look less attractive upon deeper scrutiny. Modifying 18.01 might be an appealing way to address certain problems, but the existing 18.01 curriculum is tightly coupled to the standard high school advanced placement courses and exams. Tampering significantly with 18.01 would break that correspondence and the existing advanced placement system would no longer apply.
A few possibilities are on the table for revising the introductory non-GIR mathematics subjects. Our 18.05 Introduction to Probability and Statistics can always profit from new connections to statistical problems in fields like biology and finance. Revised curricula in Engineering could have an impact on the syllabus of 18.03 Differential Equations. Communication with other departments is a vital activity in keeping these courses current and useful to our students.
We have enlisted the help of the Teaching and Learning Laboratory in our curriculum review process. A d’Arbeloff grant is providing much-appreciated support. Our timeline involves gathering input throughout the rest of this semester and into the fall term 2009, overlapping with course redesign beginning this summer and running through calendar year 2010.
Please send us your comments to: mathcore@mit.edu.
| Back to top | |
| Send your comments |
| home this issue archives editorial board contact us faculty website |