Instructor
Anastasia Yendiki, Ph.D.

Lab description
The purpose of this lab is to further familiarize you with linear-model fitting of fMRI data, in particular with the interaction of paradigm-related and nuisance components of the linear model.

Lab software
We will use NeuroLens for all fMRI statistical analysis labs.

Lab data
We will use data from the self-reference functional paradigm that was presented in Lab 1. For this lab we will use all data from Subject 7, available under the course directory: /afs/athena.mit.edu/course/other/hst.583/Data2006/selfRefOld/Subject7Sessions7-8-9-13/

Here's a reminder of the paradigm structure. Words are presented in a blocked design. Each run consists of 4 blocks, 2 with the self-reference condition and 2 with the semantic condition. The conditions alternate in the ABBA format. In particular, for Subject 7 the order is:

Run 1:  A=semantic, B=selfref
Run 2:  A=selfref,  B=semantic
Run 3:  A=semantic, B=selfref
Run 4:  A=semantic, B=selfref

10 sec   Rest
2 sec    Cue
30 sec   Block A (10 words, each lasts 3 sec)
10 sec   Rest
2 sec    Cue
30 sec   Block B (10 words, each lasts 3 sec)                
10 sec   Rest
2 sec    Cue
30 sec   Block B (10 words, each lasts 3 sec)                
10 sec   Rest
2 sec    Cue
30 sec   Block A (10 words, each lasts 3 sec)                
16 sec   Rest
----------------------------------------
TR = 2 sec
Total run duration = 184 sec (i.e., 92 scans) per run

Lab report
The lab report must include your answers to the questions found throughout the instructions below.
Due date: 12/04/2006

Lab instructions

1. As usual, open the Subject 7 data by dragging its entire folder onto the NeuroLens icon (or by starting NeuroLens and choosing Open... from the File menu):

   

2. We will first explore the impact of polynomial nuisance components on the fitting of a linear model. Open the data from the first run (Series 7) and pre-process it as you learned in the first lab. (Perform motion correction and then spatial smoothing by a Gaussian kernel with a FWHM of 6mm.)

3. Fit a linear model to the motion-corrected, smoothed images. Use the file that you created in the previous lab for the paradigm-related components of the model. This time, however, you will incorporate polynomial nuisance components of up to third order; select 3 (Cubic) from the Polynomial drift order menu in the Model tab of the Linear Modeling action.

   We want to test the statistical significance of the polynomial nuisance components. Construct a separate contrast for each of them, i.e., one contrast that selects only the constant term, one that selects only the linear term, and so on. (The Basis functions plot window in the Model tab shows you the order of the terms in the model, so it will help you in writing out the contrasts.)

   Configure the output to be -log(p) maps and run the linear model fit.

   Q: Examine the four -log(p) maps. Are the four polynomial terms of equal statistical significance? Is the statistical significance of each polynomial term uniform throughout the brain volume?

4. We will now quantify the significance of the four polynomial terms by calculating the fraction of the total voxels in the volume where each polynomial term has a statistically significant value.

   Go to the window showing the EPI images and choose the -log(p) map of one of the polynomial terms from the Overlay toolbar item at the top of the window. We will use the -log(p) map as a ROI to count the number of voxels in the volume where the -log(p) map takes an absolute value greater than 3.

   Click on the Inspector toolbar item. Click on the ROI tab of the Inspector window. Check Compute ROI Statistics. In the Thresholding box, enter 3 as the Lower bound and a value much higher than all values all the -log(p) maps (e.g., 1000) as the Upper bound. (Every time you change one of the threshold values, you will have to press TAB for the ROI statistics to be updated!) From the box of ROI statistics, record the Number of Voxels.

    

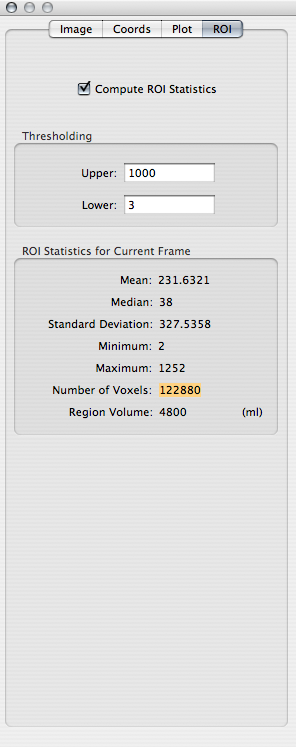
   Repeat for each of the four -log(p) maps. (Every time you change the overlay to a different map, you will have to uncheck and recheck Compute ROI Statistics for the ROI statistics to be updated!)

   Using the same method, find the number of voxels where the -log(p) map takes values less than -3. Repeat for each of the four -log(p) maps.

   Q: Record the numbers of voxels where each polynomial term is statistically significant at a -log(p) level greater than 3 or less than -3. Use these numbers to calculate the fraction of the total voxels in the 3D volume where each term is statistically significant.

   Order of poly term	#voxels > 3	#voxels < -3	(#voxels > 3 or < -3) / (# total voxels)
   0
   1
   2
   3

5. We will now explore how the addition of polynomial terms to the linear model affects inference on the paradigm-related terms of the model. We will analyze the data by gradually increasing the number of polynomial terms in the model and we will measure the significance of the model term corresponding to the self-reference condition.

   Fit a linear model to the motion-corrected, smoothed images from run 1. Specify a contrast of the self-reference condition vs. baseline. Set the Polynomial drift order to 0. Configure the output to be -log(p) maps and run the linear model fit. Save the -log(p) map of the self-reference condition vs. baseline.

   Repeat the fit three more times, each time increasing the maximum order of the polynomial drift terms to 1, 2 and 3. Save the resulting -log(p) maps.

6. We will now measure the maximum of the -log(p) map within certain ROIs as a function of the maximum order of the polynomial drift terms in the linear model.

   Open the visual cortex ROI that you will find under /afs/athena.mit.edu/course/other/hst.583/Data2006/selfRefOld/subj7,run1,roi,visual,lab7ii.mnc

   To locate the ROI in the 3D volume, you can check Show all slices at the bottom of the window displaying the ROI file:

   

   Command-click on some voxel within the ROI and check the statistical maps to make sure that the ROI corresponds to a cluster of active voxels. Go back to the window displaying the ROI file. From the Action toolbar item, choose ROI Statistics. A window will appear with a list of all open files (except the ROI file itself):

   

   In the window above you have to choose the images from which you want to extract ROI statistics. Select the four -log(p) maps of the self-reference-vs.-baseline contrast that you obtained in the previous step. (In the list of file names, you can Shift-click to select a set of file names or Command-click to add a file name to the selection.)

   Enter 1 as the Lower threshold (and then press TAB as usual!) This will make sure that the statistics are only calculated over the voxels where the ROI takes a non-zero value. (If you left the lower threshold set to 0, you would get statistics from the entire 3D volume.) Leave the Upper threshold as is.

   Click on the OK button to compute ROI statistics in the four statistical maps. The result should come up in a window like the following:

   

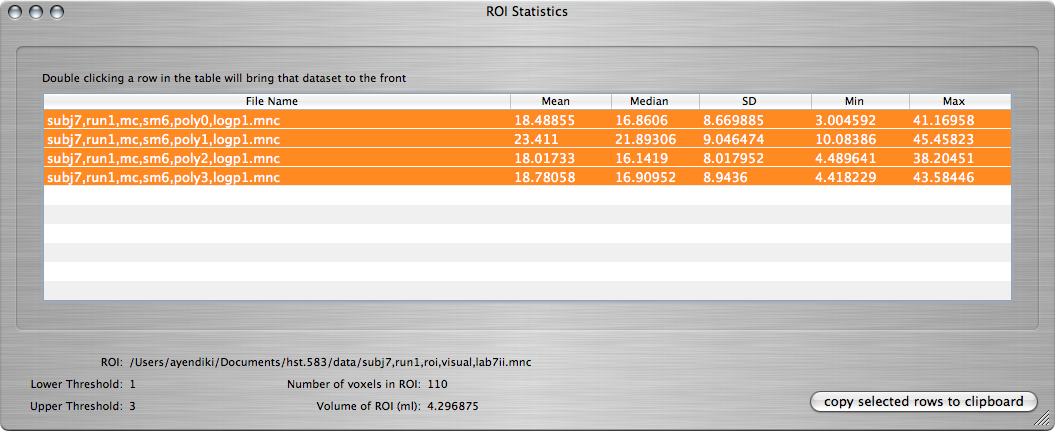
   Q: Record the maximum value of the -log(p) map within the visual-cortex ROI as a function of the maximum order of polynomial drift terms in the linear model.

   To copy the values directly to your lab report, you can select all four rows, click on the copy selected rows to clipboard button, and then paste to your document. You only need to keep the last value (Max) from each row.

7. Repeat the previous step for three more ROIs.

   • ROI in the motor cortex: /afs/athena.mit.edu/course/other/hst.583/Data2006/selfRefOld/subj7,run1,roi,motor,lab7ii.mnc
   • ROI in the medial prefrontal cortex (MPFC): /afs/athena.mit.edu/course/other/hst.583/Data2006/selfRefOld/subj7,run1,roi,mpfc,lab7ii.mnc
   • ROI in the cerebellum: /afs/athena.mit.edu/course/other/hst.583/Data2006/selfRefOld/subj7,run1,roi,cerebel,lab7ii.mnc

   Q: Record the maximum value of the -log(p) map within each ROI as a function of the maximum order of polynomial drift terms in the linear model.

   Highest-order poly term	Max -log(p) visual	Max -log(p) motor	Max -log(p) MPFC	Max -log(p) cerebellar
   0
   1
   2
   3

   Q: Show plots of the maximum -log(p) vs. polynomial order for each of the four ROIs. Do all ROIs exhibit the same trend as the order of the polynomial drift terms increases? If you had to choose the maximum polynomial order in your model based on the comparisons that you performed in this lab, what would you choose?