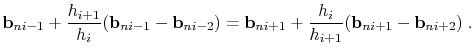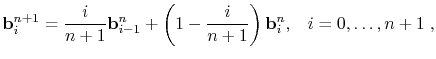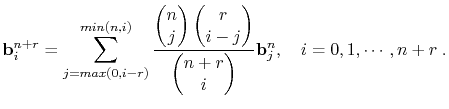| (1.44) |
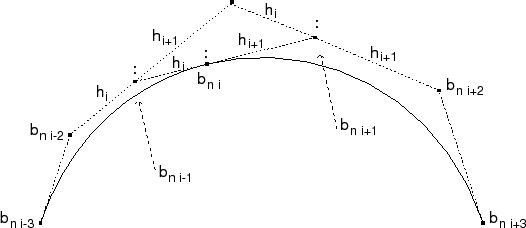
is applied recursively to obtain the new control points. The algorithm is illustrated in Fig. 1.6, and has the following properties:
- The values
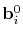 are the original control points of the curve.
are the original control points of the curve.
- The value of the curve at parameter value
 is
is
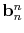 .
.
- The curve is split at parameter value
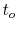 and can be represented as
two curves, with
control points
and can be represented as
two curves, with
control points
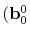 ,
,
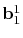 ,
, ,
,
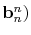 and
and
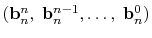 .
.
One set of continuity conditions are the geometric continuity
conditions, designated by the letter ![]() with an integer exponent. Position continuity, or
with an integer exponent. Position continuity, or ![]() continuity, requires the endpoints of the two curves to coincide,
continuity, requires the endpoints of the two curves to coincide,
| (1.45) |
The superscripts denote the first and second curves. Tangent continuity, or
| (1.46) | |||
| (1.47) |
where
Curvature continuity, or ![]() continuity, requires
continuity, requires ![]() continuity
and in addition the center of
curvature to move continuously past the connection point [116],
continuity
and in addition the center of
curvature to move continuously past the connection point [116],
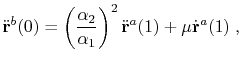 |
(1.48) |
where
More stringent continuity conditions are the parametric
continuity conditions, where ![]() continuity requires the
continuity requires the ![]() th derivative (and all lower derivatives) of each curve to be equal at
the joining point. In other words,
th derivative (and all lower derivatives) of each curve to be equal at
the joining point. In other words,
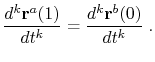 |
(1.49) |
Let us assume that the global parameter ![]() , associated with the
, associated with the
![]() -
-![]() segment of a composite degree
segment of a composite degree ![]() Bézier curve with local
parameter
Bézier curve with local
parameter ![]() (
(
![]() ), runs over the interval
), runs over the interval ![]() ,
,
![]() . Then the
. Then the ![]() -
-![]() segment of a composite Bézier curve
is given by:
segment of a composite Bézier curve
is given by:
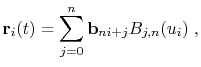 |
(1.50) |
where the global parameter
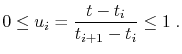 |
(1.51) |
If we denote
and
Figure 1.7 illustrates the connection of two cubic Bézier curve segments at
where