|
|
in Electromagnetism 2000 |
Vision |
|---|---|---|
| Motivation | ||
| Examples | ||
| Value Added |
Time Frame |
|
| Table of Contents |
|
|
in Electromagnetism 2000 |
Vision |
|---|---|---|
| Motivation | ||
| Examples | ||
| Value Added |
Time Frame |
|
| Table of Contents |
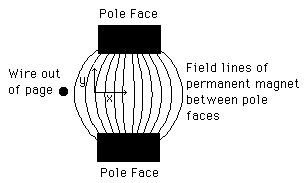
 1.5 Meg MPEG
1.5 Meg MPEG
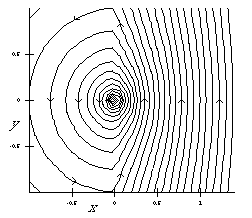
 0.5 Meg MPEG
0.5 Meg MPEG
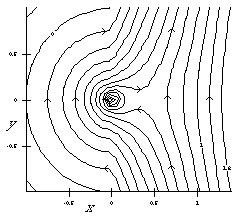
 1.2 Meg MPEG
1.2 Meg MPEG
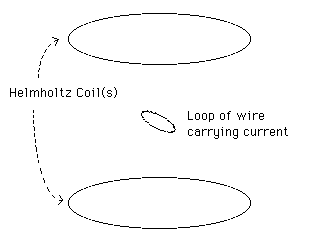
 1.1 Meg MPEG
1.1 Meg MPEG
![[next]](next.gif)
![[previous]](previous.gif)
![[Page Top]](pagetop.gif)
![[contents]](contents.gif)