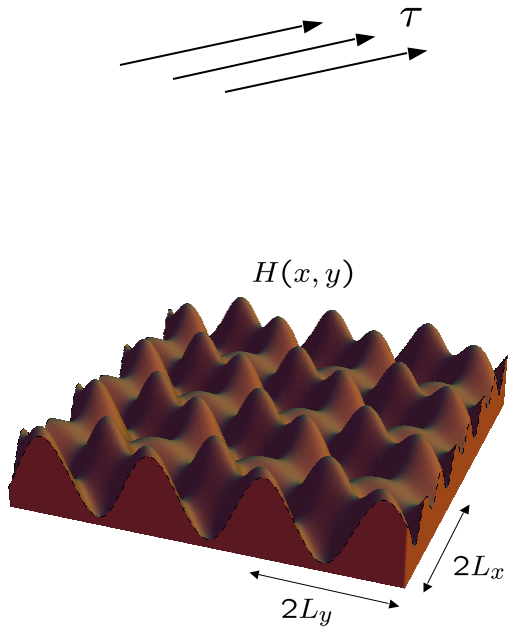
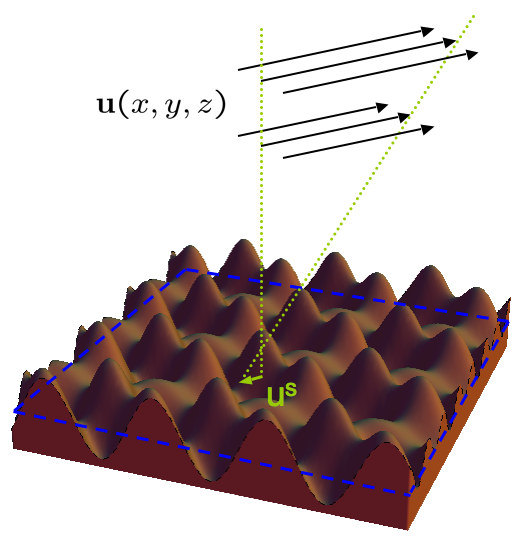
Complementing our efforts on computation, we have a number of projects where the focus is on analytical studies to derive approximate formulas, constraints, or reduced-order models within certain families of mechanics and materials problems. We describe a few such projects below.

Recent work in the fabrication of microfluidic devices has motivated interest in quantifying the effects of surface texture on bulk low-Reynolds-number fluid flow. In non-trivial ways, wall patterning can be used to impede or expedite adjacent fluid motion, causing non-negligible far-away effects. One basic goal is to extract a homogenized boundary condition for the smooth, mean surface, that mimics the effects of the actual condition along the true, corrugated surface. We have carried out an analytical/perturbative study resulting in a second-order formula, complete with error bound, that converts any such surface to an effective tensorial mobility law on the mean surface.  We have followed up with additional analytical results pertaining to the symmetry of mobility tensors for arbitrary patterned surfaces, and special identities that arise relating to flows over striped patterns.  This work has recently extended to the non-Newtonian limit producing a family of nonlinear Onsager-like symmetry constraints on the relations that emerge.

On another front, we have derived analytical expressions for the so-called "En-Passant" crack growth problem, a family of two-crack geometries which connect to the process by which crack networks form. En-Passant cracks begin as a pair of parallel, offset cracks that grow toward each other when far-field loading is applied. They are commonly occuring in nature, and can be found in large-scale on the earth's crust, as well as in common asphault. Calculating the paths of these cracks requires solving a mathematically daunting integral equation system, as the mutual growth process continuously changes the global stress field and therefore the next growth increment. By applying boundary integral methods and pertubration theory, we have obtained and validated an analytical formula for short growth paths.

We have derived a 1D elasto-viscoplastic filament model which permits reduced-order modeling of highly deforming filaments or sheets made of rheologically complex media (gels, foams, pastes, etc). This extends nonlinear beam theory for elastica to elasto-viscoplastic media, which may contain a yield stress and/or rate-dependent plastic flow rule. We have demonstrated the accuracy of our model using a variety of viscoplastic catenaries, wherein thin horizontal sheets of complex media droop over time due to gravity. The model demonstrates correct time-dependence of the droop, and accurately predicts the distribution of plastic strain through the thickness without explicit modeling in the thickness dimension.

External collaborators:

Howard Stone (Princeton)
Joe Goddard (UCSD)
L. Mahadevan (Harvard)

Back to main page.

Fluid is sheared over an arbitrary (periodic) textured surface. The "effective slip" velocity u^s is computed from the surface corrugations and can be used as a macroscopic boundary condition.

En-Passant crack growth within the Earth's crust (Acocella et. al (2000)). Whether cracks initially curve away or toward each other can be calculated as a result of their initial separation and far-away loading state.

Top: The drooping rheo-catenary setup. Bottom: Three snapshots in time of (left) a 3D finite-element simulation of a drooping elasto-viscoplastic filament with yield stress, where the contours show the plastic strain-rate, and (right) the same problem calculated in a fraction of the time using the 1D model, with red coloration indicating where the model predicts the plastically flowing zones to exist.