Theory

 

I. Alpha-Helices: Building Block of Cells

 

Proteins constitute the critical building blocks of life, providing essentially mechanical functions to biological systems, and the focus of many molecular and atomistic level simulations. In particular, alpha-helical (AH) protein domains are the key constituents in a variety of biological materials, including cells, hair, hooves and wool.

 

The alpha helix is a secondary structure in proteins. This means that it results from the folding of a single amino acid chain. Hydrogen bonds form between segments of the chain, creating this folded morphology. Specifically, the amine groups in the amino acid backbone bond with a carbonyl group. The alpha helix measures about 5.4 Å in width and are about 10 amino acids long. It is tightly packed and therefore behaves like a spring.

 

While continuum mechanical theories have been very successful coupling the atomistic and macro scales for crystalline materials, biological materials and soft condensed matter (such as polymer composites) require different approaches to describe elasticity, strength, and failure. The fundamental deformation and failure mechanisms of biological protein materials remain largely unknown, due to a lack of understanding of how individual protein building blocks respond to mechanical load.

 

 

 

To download this application, press on the link above.

 

Once launched, the application is dynamic and constantly running.

 

Clicking within the blue simulation box will apply a horizontal force to the alpha-helix protein via the atomic force microscopy (AFM) tip (silver triangle). Drag the force to the right to increase the length of the alpha-helix and induce unfolding of the coils.

 

Above the simulation lies a value that indicates the length of the segment. This value will increase as you pull on the alpha helix. The force value portrays the increasing force applied on the alpha helix due to the pulling. The user can control the probe and pull the alpha helix until the protein structure is strained to a breaking point. When the force reaches a threshold value, the structure of the protein unwinds.

 

In this simulation, we mimic the experimental process of atomic force microscopy (AFM) on the stretching and unfolding of an alpha-helical protein.

 

It has been determined both experimentally [1] and via simulation [2] that the mechanical response of biological materials is a combination of molecular unfolding or sliding, with a particular significance of rupture of reversible chemical bonds such as hydrogen bonds (shown in yellow in the simulation). The hydrogen bonds stabilize the helical structure of the alpha helix - when unfolding, the hydrogen bonds are broken.

 

Once completely unfolded, the load is taken by the backbone of the protein (thick purple lines in the simulation) and it takes a lot more force to stretch the protein. Unlike man-made materials, nature’s building blocks get stronger as they are deformed!

 

 

 

 

 

 

 

Program Author(s):

 

 

Webpage Author(s):

 

 

Advisor:

 

 

 

[1] Dietz, H., et al., Anisotropic deformation response of single protein molecules. Proceedings of the national Academy of Sciences, 2006. 103(34): p. 12724-12728.

 

[2] Ackbarow, T., et al., Hierarchies, multiple energy barriers, and robustness govern the fracture mechanics of alpha-helical and beta-sheet protein domains. Proceedings of the National Academy of Sciences, 2007. 104(42): p. 16410-16415.

 

[3] Qin, Z., L. Kreplak, and M.J. Buehler, Hierarchical structure controls nanomechanical properties of vimentin intermediate filaments. PLos ONE, 2009. 4(10): p. e7294.

 

 

[5] Bertaud, J., Z. Qin, and M.J. Buehler, Atomistically informed mesoscale model of alpha-helical protein domains. International Journal for Multiscale Computational Engineering, 2009. 7(3).

 

[6] Bertaud, J., et al., Energy landscape, structure and rate effects on strength properties of alpha-helical proteins. Journal of Physics: Condensed Matter, 2009.

 

The bond potential can describe the microscopic details of the rupture mechanism of the convolution H-bonds under force, as well as the transition from a folded to unfolded state, through the prescribed energy barrier of the potential. The description is sufficiently coarse to enable significant computational speedup and efficiency compared with a full atomistic description.

III. Unfolding

 

The remaining question: How can we representing the unfolding behavior by a simple bead-spring representation?

 

Short answer: Change the bond stiffness based on particle separation.

 

Long answer:  The potentials must represent the structural backbone protein domain, and also the energetic features of the stabilizing hydrogen bonds. One of the interesting features of this simulation is the energy landscape. As mentioned, each alpha helix is tightly bound and therefore stores considerable energy in its bonds. In order for an alpha helix to unwind, an outside force must break an energy barrier associated with each convolution.

 

In general, molecular structures tend toward the lowest energy configuration. In this case, the minimum energy state (labeled with a purple point in Fig. 3) corresponds to folded state of the alpha helix, which is the most favorable. When a pulling force is applied to the system, the bond potential increases, reaching a local maximum (Eb) where the hydrogen bonds of the alpha helix are broken. Immediately, the structure reaches a new equilibrium state (labeled with a blue square), corresponding to a decreased bond potential (Er).

 

The aim is to capture the structural and energetic features of an AH protein domain. A double-well potential was developed to capture the existence of two equilibrium states for a convolution: folded and unfolded (See Figure 3). The breaking dynamics of AH convolutions is captured by the effective double-well potential, parameterized by full atomistic simulations that implemented explicit solvent.

 

It is important to note that alpha helices have an essential role in the stability of larger protein structures. Studies have shown that the breaking of the alpha helix in a protein can lead to local unwinding and loss of function [4]. Alpha helices are also important in the binding of DNA. Therefore, studying the failure of alpha helices can help understand malfunctions in certain biological systems.

 

Even a small protein structure of a single alpha-helix requires a lot of atoms for a full atomistic representation. The simulation above implements a coarse-grain, or “super-atom” representation of an alpha-helical protein.

 

II. Coarse-Grain “Mesoscopic” Model

 

 

The setup of the coarse-grain model for AH protein domains is based on the geometry of an AH, which features a linear array of turns or convolutions stabilized through the presence of H-bonds between sequential amino acid residues. During mechanical loading, any one of these convolutions can possibly rupture. As such, the coarse-grain representation is rationally discretized into bead-spring elements representing a single convolution (turn). To achieve the coarse-grained description, the entire sequence of amino acids that constitute the AH is replaced by a collection of mesoscopic bead-spring elements (See Figure 2).

 

Figure 1: Hierarchies of Alpha-Helical Structures

 

Schematic depicting hierarchical structure of alpha-helix protein-based intermediate filaments (IFs), which provide structural tensegrity to the cytoskeleton of cellular membranes. Over seven levels of hierarchy are transcended, from hydrogen bonds, to alpha-helical turns, alpha-helical proteins (which are the focus of coarse-graining discussed here), dimers (coiled-coiled protein domain), tetramers, unit-length filaments, full-length filaments to the cellular level. Figure adapted from [3].

 

 

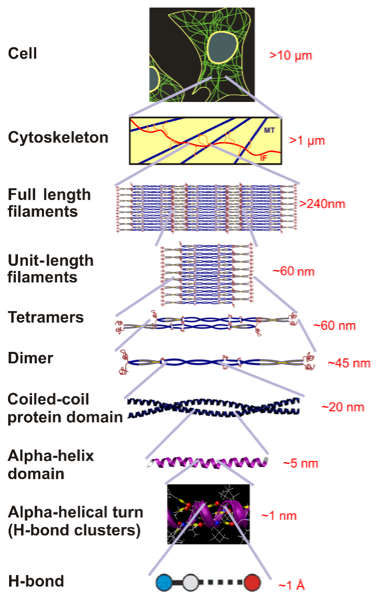
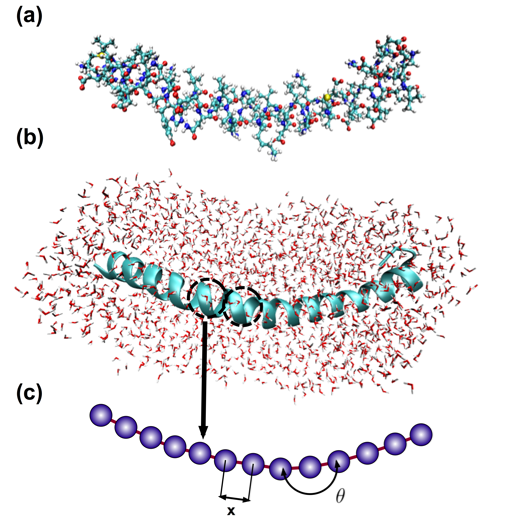
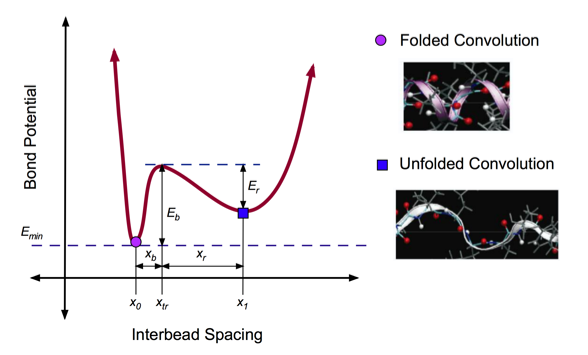
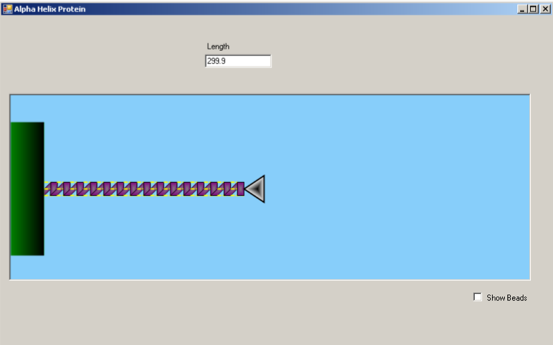
Figure 2: Full Atomistic v. Coarse-Grain Models

 

Schematic of coarse-graining procedure, in which full atomistic representation is replaced by a mesoscopic bead-spring model. A pair of beads represents one turn in the alpha-helix (also called a convolution), and thus 3.6 residues with the corresponding mass. (a) Full atomistic representation depicting all atoms and bonds; folded states of the turns are stabilized by the presence of hydrogen bonds between residues (not shown); water molecules not shown for clarity. (b) Ribbon representation of protein, illustrating alpha-helical folded conformation of backbone chain and individual convolutions; explicit solvent (water molecules) shown. (c) Developed coarse-grain representation, with a single bead per convolution; need for explicit solvent eliminated in coarse-grain model, as effects are integrated into coarse-grain potentials.

 

 

 

Figure 3: Double-Well Potential for Unfolding

 

Double well profile of the bond stretching potential of the coarse-grain model, representing the energy landscape associated with unfolding of one convolution. The values of the equilibrium states, x0 and x1, energy barriers, Eb and Er, and the transition state, xtr, are obtained from geometric analysis of the alpha-helix geometry, as well as the full atomistic simulations. The transition state (local energy peak) corresponds to the breaking of hydrogen bonds between convolutions of the alpha-helix. After failure of these weak bonds, the convolution unfolds to a second equilibrium state with a large inter-particle distance. Under further loading, the covalent bonds begin to stretch, which leads to a second increase of the potential at large deformation.