Theory
This simulation will display the behavior of atoms due to changes in temperature. Fundamentally, it attempts to link the equilibrium distance of bonded atoms with the temperature. Running the simulation, as you increase the temperature, the velocity of atom increases, as does their distance from the central, fixed atom. This behavior is modeled by the Maxwell-Boltzman distribution for velocities, and the Lennard-Jones Potential for atomic bonding.
Crystal Structures
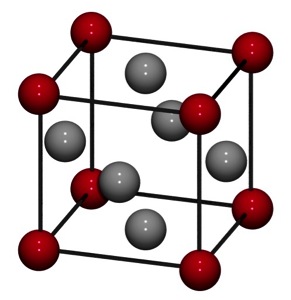
In this simulation, we include four atoms of equal mass. These are free to move in respond to changing conditions, in this case, changing temperature. A fifth atom is fixed at the center. This arrangement was not random, as we attempt to represent a single face of a face-centered cubic (FCC) crystal structure.
Thermal Expansion

Simulation Instructions
To download this application, press on the link above.
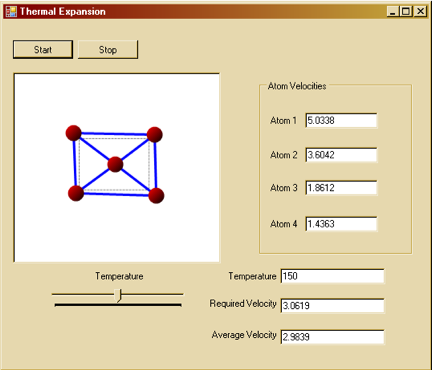
For each application, press the “Start” button to activate the simulation and the “Stop” button to pause it.
To change the temperature in the simulation, use the scroll bar located at the bottom of the window.
Simulation Description
In this simulation, we simplify a atomistic crystal structure in an attempt to show atom behavior at a basic level, which can help understand the behavior of a more complex system of atoms.
Particularly, this application demonstrates how a simple assembly of bonded atoms reacts to changes in temperature via a change in atom velocity (kinetic energy), illustrating that higher temperatures (I.e. increase in energy) results in an increase in volume of the atomistic structure – a.k.a. thermal expansion.
The interface of the program provides a scroll bar to manipulate the temperature in the simulation. By incrementing and reducing its value, you can get a general sense of how atoms behave at different temperatures and velocities.

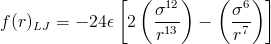
Credits
Program Author(s):
Webpage Author(s):
Advisor:
Citations
[1] Iacovella, Christopher R. (2006). Face Centered Cubic (FCC) unit cell. Glotzer group. Depts of Chemical Engineering, Materials Science & Engineering, Macromolecular Science, and Physics, University of Michigan.
[2] Ziman, J.M. (1972). Principles of the Theory of Solids, 2nd Ed. Cambridge University Press. ISBN 0521297338 9780521297332
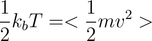






Copyright (c) 2009 Laboratory of Atomistic and Molecular Mechanics. All rights reserved.

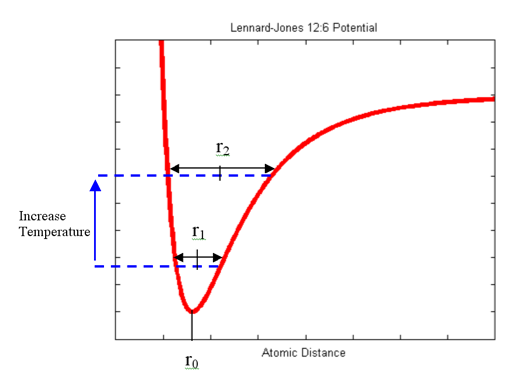

At a lower temperature, the atom vibrates about an equilibrium distance equal to r1.
Increasing the temperature (adding energy to the system), the atom vibrates about an equilibrium distance equal to r2.
The potential energy “flattens” at a higher rate due to the relative decay of the repulsive term compared to the attractive term (resulting in an anharmonic potential), resulting in r2 being greater than r1.
With each corresponding vibrational energy level, the atom vibrates about an equilibrium spacing, which minimizes the free energy of the system.
This equilibrium spacing increases with vibrational (a.k.a. kinetic energy), which is proportional to temperature - thus, thermal expansion!
Note that the “<>” brackets indicate the average kinetic energy of each atom in the system.
For our simple system of four moving atoms, it is easy to calculate the average kinetic energy at every time step, so we can calculate the temperature.
To achieve a desired temperature is a little more challenging.
In any system, all of the atoms do not move at the same velocity. The atoms have a range of different velocities, and the velocity of any single atom constantly changes due to interactions with other particles. However, the fraction of a large number of atoms (or molecules) within a particular velocity range is nearly constant if the system is at or near equilibrium, thus leading to temperature. To simulate these fluctuations, we define the initial velocities of the system randomly according to a Maxwell–Boltzmann distribution (which is a normal distribution for velocities) about a desired mean. The Maxwell distribution of velocities specifies this fraction, for any velocity range, as a function of the temperature of the system.
After each timestep, we can then scale the actual velocities of each atom (which are random) according to the desired mean velocity (from the Maxwell-Boltzmann distribution), to attempt to attain the desired temperature. That is why in the simulation, there is a slight difference between required velocity and average velocity. The required velocity is the velocity calculated from the temperature-velocity relation, while the average velocity is calculated based on the actual, random velocities of the atoms at each timestep.
Thermal Expansion
The remaining question: Why does a material expand when there is an increase in temperature?
Short answer: An increase in energy results in an increase in equilibrium spacing of the atomic bonds.
Long answer: Thermal expansion is due to the anharmonicity of the atom interactions [2]. As the temperature rises the amplitude of the crystal lattice vibrations increases, but the equilibrium distance shifts as the atoms spend more time at distances greater than the original spacing due as the repulsion at short distances is greater than the corresponding attraction at farther distances.
Conceptually, when the temperature is increased, you can think of the potential energy of the system “filling” the energy well of the bonding potential:
The four moving atoms repel when close to the center atom and attract when farther apart. As long as there is kinetic energy (when the atoms are moving), these forces will maintain the atoms vibrating about their equilibrium distance.
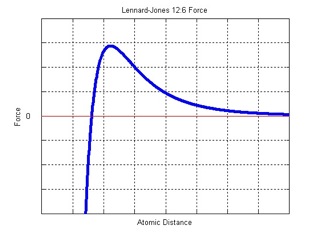
For simplicity, only the interaction between each atom and its nearest neighbor (i.e. the center atom) is considered in this simulation. Physically, each atom will be affected by all the atoms surrounding it. However, as shown in the above plot, the force due to each atom decreases rapidly with distance. Usually, in molecular dynamics, a cut-off is implemented, and atoms outside this region are negligible and ignored.
Click here for more information on the Lennard-Jones Potential.
Temperature and Atomic Velocity
The temperature of any (massive) physical system is the result of the motions of the molecules and atoms which make up the system. We can link the temperature and velocities of an atomic system via the average kinetic energy of the atoms, where:
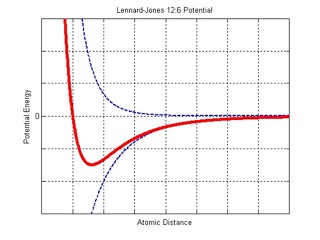
Where “r” is the distance between atoms. The atoms like to be in the bottom of the energy well (the “bowl” in the above plot), and at that minimum, the distance between two atoms is known as their equilibrium distance - any closer, and the atom gets repelled, and farther and the atom is attracted.
The Lennard-Jones Potential is empirical - it is used because it closely fits experimental results and quantum mechanical data. Essentially, it represents a balance between attractive and repulsive energies between two atoms (depicted as dashed blue lines in the plot above).
This equation also describes the forces that arise between any two neutral atoms: an attractive force at long ranges and a repulsive force at short ranges. Forces can be calculated by taking the derivative of the Lennard-Jones Potential:
Such an atomic arrangement is common in many metals, including copper (Cu), gold (Au), silver (Ag), and nickel (Ni).
In reality, each corner atom would also be bonded to atoms in adjacent crystals, but we have neglected those to simplify our simulation. Further, in reality, the center atom is free to move like the corner atoms. We fix the center atom for visualization purposes (i.e. a consistent basis to compare thermal expansion).
Atomic Bonding
The atomic interaction for this simulation is defined by the Lennard-Jones Potential:
Face centered cubic [1]