Measure

 

---

Units

PML will drive its units from the fundamental units of measure developed by the International Bureau of Weights and Measures (Le Système International d'Unités or SI) in conjunction with others such as the National Institute of Standards and Technology (NIST) in the United Sates.

Although the SI units form the basis, the PML specification modifies and expands those to accommodate the particular needs of industry, commerce and consumer applications. In particular quantity (dimensionless measure of units), angle (dimensionless measure of angle in radians) and percent were added to facility the communication of common dimensionless values.

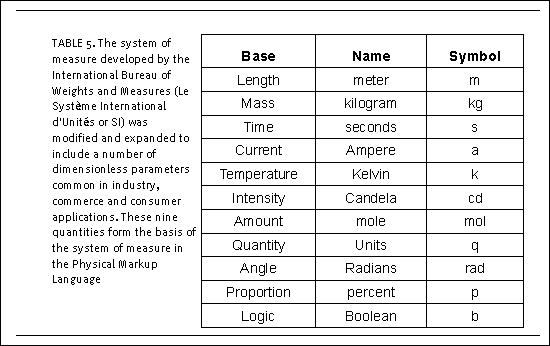
The eleven units forming the basis of the PML measurement specification are shown below in See The system of measure developed by the International Bureau of Weights and Measures (Le Système International d'Unités or SI) was modified and expanded to include a number of dimensionless parameters common in industry, commerce and consumer applications. These nine quantities form the basis of the system of measure in the Physical Markup Language.

Most physical properties will be products of these base units. Speed, for example, is the ratio of length to time, viscosity may be defined in kilograms per meter seconds and power kg m² s^-3.

PML defines a measure element, msr , which contains a single floating-point number. The msr element includes nine optional attributes m, kg, s, a, K, cd, mol, q, rad, p and b which define the exponent of the unit of measure. If an exponent attribute is omitted it is assumed to be zero.

The two quantities just mention, speed, for example, would be written as <msr m=1 s=-1> and viscosity would be <msr kg=1 m=2 s=-3> . The advantage is that unit conversion and measurement ambiguity are eliminate.

 

---

Accuracy

Measurements, of course, are not always accurate. Using a ruler you can measure to within 0.1 of an inch, with a caliper to within 0.001 in and with a micrometer to within 0.0002. We need some means of specifying accuracy within the measurement specification of the Physical Markup Language.

There are many ways to specify tolerances. Again keeping with our philosophy of one simple, yet usable specification, this version of PML uses a just a minimum and maximum tolerance.

Therefore we introduce attributes into the msr element: a tolerance specification min and max , representing the minimum and maximum tolerance of the measurement.

<msr min= float max= float > float </msr>

In other words, the actual value lies somewhere between the specified value less the min value and the specified value plus the max.

If the attributed min is missing, the actual value is interpreted to lie within the specified measurement plus or minus the max value.

<msr max= float > float <msr>

We include in the measurement specification a simple label attribute containing a string, which simply describes the type of measurement, such as "ambient temperature" or "nominal weight"

<msr label= string > float </msr>

---

Intention

Often we want to specify a measurement concept, such as 1 foot - exactly one foot not 0.3048 meters. We may want those with whom we communicate to understand a measurement concept - such as "one foot." If we translate into a common standard, how can we be assured this concept will be preserved during the communication?

Fortunately there is enough information in the PML definition to convey this intent. We can use the tolerance together with a flag signaling the receiver to "latch" a data value to the nearest increment within the bounds of the tolerance - in other words, to round to the nearest unit.

For example, suppose we convert the intention of 1 foot to the PML specification of 0.3048 meters. If we include a tolerance of say 0.001 meters (or one millimeter) together with flag indicating the receiver should "latch" to the nearest unit, then a conversion to Imperial units would yield 12 inches or 1 foot - exactly.

To communicate this intent, we introduce a latch attribute, which accepts a Boolean value of either "true" or "false".

<msr latch= boolean > float </msr>

---

Arrays

Multiple data values - even streaming telemetry - can be communicated efficiently with the array element.

The array element includes one or more msr elements. The number msr elements defines the dimension of the array, the attributes of the individual elements define the units and range of each dimension, and the value of the msr element is the offset of initial condition of the data values. We also include a label attribute describing the array.

Following the msr elements are a list of float point vectors. These vectors are denoted by a list of floating point numbers separated by spaces, and the vectors themselves separated by commas. The dimension of the vectors must match the number of msr elements.

<array label=string >

<msr label=string > float </msr> (Dim 1)

. . . . . .

<msr label=string > float </msr> (Dim n)

float₁ float₂ . . . float_n ,

float₁ float₂ . . . float_n ,

. . .

float₁ float₂ . . . float_n

</array>

 

 

 

 The array element provides another method for recording data. The optional attribute periodic allows measurements with respect to regular, periodic input. The periodic attribute accepts a single integer representing the number of independent variables.

If periodic is set to 1, for example, the array element assumes measurements with respect to a single independent variable. If periodic is set to 2, measurements are assumed to be with respect to two indendent variables - a grid or surface map are good examples.

The array element allows an arbitrary number of dependent variables for every measurement. In other words, for every independent data value, there may be one or more output values .

Since the array element allows one or more periodic input variables, the specification must record the offset and frequency of these variables, as well as the number of measurements along each dimension.

Following the array declaration, there are pairs of msr elements representing the initial value and period of each independent dimension. There is also a size element, which simply storages an integer representing the number of measurements along that dimension. Thus if the periodic attribute is set to m , there will be m pairs of msr elements and m size elemnts as follows

<array label=string periodic=integer >

<msr> float </msr> (offset 1)

<msr> float </msr> (period 1)

<size> integer </size> (size 1)

. . .

<msr> float </msr> (offset m)

<msr> float </msr> (period m)

<size> integer </size> (size m)

 

Following the specification of the independent variables, the array element expects one or more msr elements representing the number and offsets of the dependent variables.

<array label=string periodic= integer >

<msr> float </msr> (offset 1)

<msr> float </msr> (period 1)

<size> integer </size> (size 1)

. . .

<msr> float </msr> (offset m)

<msr> float </msr> (period m)

<size> integer </size> (size m)

<msr> float </msr> (dimension 1)

. . .

<msr> float </msr> (dimension n)

The data is stored in vectors. The vectors are separated by commas and their component values are separated by white space. Assuming there are m independent variables and k_i elements for the i th indenpendent variable, there will be n -dimensional vectors. The general form of the array element is as follows:

<array label= string periodic= integer >

<msr> float </msr> (offset 1)

<msr> float </msr> (period 1)

<size> integer </size> (size 1)

. . .

<msr> float </msr> (offset m)

<msr> float </msr> (period m)

<size> integer </size> (size m)

<msr> float </msr> (dimension 1)

. . .

<msr> float </msr> (dimension n)

 

float₁ float₂ . . . float_n ,

float₁ float₂ . . . float_n ,

. . .

float₁ float₂ . . . float_n

</array>

 

---

Units

The following table illustrates some of the commonly used units and their representation in the Physical Markup Language.

 

Quantity	Name	Symbol	PML Units
Area	square meter		m=2
Volume	cubic meter		m=3
Speed	meter/second		m=2 s=-1
Accelearation	meter/second2		m=2 s=-2
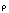
Mass density	kilogram/meter3		kg=1 m=-3
Specific volume	meter3/kilogram		kg=1 m=-3
Current density	Ampere/meter2		a=1 m=-2
Magnetic field strength	Ampere/meter		a=1 m=-1
Concentration	moles/meter3		mol=1 m=-3
Luminance	Candela/meter2		cd=1 m=-2
Solid angle	Steradian	sr	rad=1
Frequency	Hertz	Hz	s=-1
Force	Newton	N	m=1 kg=1 s=-2
Pressure	Pascal	Pa	m=-1 kg=1 s=-2
Energy	Joule	J	m=2 kg=1 s=-2
Power	Watt	W	m=2 kg=1 s=-3
Charge	Coulomb	C	a=1 s=1
Potential	Volt	V	m=2 kg=1 s=-3 a=-1
Capacitance	Farad	F	m=-2 kg=-1 s=4 a=2
Resistance	Ohm		m=2 kg=1 s=-3 a=-2
Conductance	Siemens	S	m=-2 kg=-1 s=3 a=2
Magnetic Flux	Weber	Wb	m=2 kg=1 s=-2 a=-1
Flux density	Tesla	T	mg=1 s=-2 a=-1
Inductance	Henry	H	m=2 kg=1 s=-2 a=-2
Temperature	Kelvin	K	k=1
Luminous flux	lumen	lm	cd=1
Illuminance	Lux	lx	m=-2 cd=1
Absorbed dose	Gray	Gy	m=2 s=-2
Dose equivalent	Sievert	Sv	m=2 s=-2
Catalytic activity	Katal	kat	s=-2 mol=1
Viscosity	Pascal second		m=-1 kg=1 s=-1
Torque	Newton meter	Nm	m=2 kg=1 s=-2
Surface tension	Newton/meter	N/m	kg=1 s=-2
Angular velocity	Radians/second	rad/s	rad=1 s=-1
Angular acceleration	Radians/second2	rad/s2	rad=1 s=-2
Heat flux density	Watt/meter2	W/m2	kg=1 s=-3
Entropy	Joule/Kelvin	J/K	m=2 kg=1 s=-2 k=-1
Specific entropy	Joule/(Kelvin kilogram)	J/(K kg)	m=2 s=-2 k=-1
Specific energy	Joule/Kilogram	J/kg	m=2 s=-2
Thermal conductivity	Watt/(Kelvin meter)	W/(K m)	m=1 kg=1 s=-3 k=-1
Energy density	Joule/meter3	J/m3	m=-1 kg=1 s=-2
Electric field strength	Volt/meter	V/m	m=1 kg=1 s=-3 a=-1
Electric charge density	Coulomb/meter3	C/m3	m=-3 a=1 s=1
Electric flux density	Coulomb/meter2	C/m2	m=-2 a=1 s=1
Permittivity	Farad/meter	F/m	m=-3 kg=-1 s=4 a=2
Permeability	Henry/meter	H/m	m=1 kg=1 s=-2 a=-2
Molar energy	Joule/mole	J/mol	m=2 kg=1 s=-2 mol=-1
Molar entropy	Joule/(mole Kelvin)	J/(K mol)	m=2 kg=1 s=-2 mol=-1 k=1
X-Ray Exposure	Coulomb/kilogram	C/kg	a=1 s=1 kg=-1
Absorbed dose rate	Gray/second	Gy/s	m=2 s=-3
Radiant intensity	Watt/Steradian	W/sr	m=2 kg=1 s=-3 rad=-1
Radiance	Watt/(meter2 Steradian)	W/(m2 sr)	kg=1 s=-3 rad=-1
Catalytic concentration	Katal/meter3	kat/m3	m=-3 s=-2 mol=1

 

---

Conversions

---

Specification: Measure

The elements and attributes of the msr (measurement) element are given below.

 

<msr label=string latch=boolean

m=integer

kg=integer

s=integer

a=integer

mol=integer

q=integer

cd=integer

rad=integer

p=integer

b=integer

min=float max=float >

float

</msr>

 

---

Specification: Array

 

<array label=string >

<msr label=string > float </msr> (Dim 1)

. . . . . .

<msr label=string > float </msr> (Dim n)

float₁ float₂ . . . float_n ,

float₁ float₂ . . . float_n ,

. . .

float₁ float₂ . . . float_n

</array>

 

<array label=string periodic=integer >

<msr> float </msr> (offset 1)

<msr> float </msr> (period 1)

<size> integer </size> (size 1)

. . .

<msr> float </msr> (offset m)

<msr> float </msr> (period m)

<size> integer </size> (size m)

<msr> float </msr> (Dim 1)

. . .

<msr> float </msr> (Dim n)

float₁ float₂ . . . float_n ,

float₁ float₂ . . . float_n ,

. . .

float₁ float₂ . . . float_n

</array>