PHENOMENA OF THE HEAVENS
Proclamation of the New Mechanics. --- Verification of Theoretical Results. --- Parallels with Leverrier. --- Neptune and Mercury. --- Testing the Theory of Relativity. --- The Solar Eclipse of 1919. --- The Programme of an Expedition. --- The Curved Ray of Light. --- Refinement of Calculation and Measurement. --- Stellar Photography. --- The Principle of Equivalence. --- The Sun Myth.

Henri Poincaré ca. 1910.
On the 13th October 1910 a memorable event took place in the Berlin Scientific Association : Henri Poincaré, the eminent physicist and mathematician, had been announced to give a lecture in the rooms of the institute "Urania" ; an audience of rather meagre dimensions assembled.
I still see him before me in my mind's eye, a scholar who was snatched away in the prime of his creative period, a man whose external appearance did not suggest the light of genius, and whose carefully trimmed beard reminded one rather of the type of a practising barrister. He walked up and down the platform, accompanying his speech with gestures marked by an easy elegance. There was no sign of an attempt to force a doctrine. He developed his thesis, in spite of the foreign language, in fluent and readily intelligible terms.
It was at this lecture that we heard the name Albert Einstein pronounced for the first time.
Poincaré's address was on the New Mechanics, and was intended to make us acquainted with the beginning of a tendency which, he himself confessed, had violently disturbed the equilibrium of his former fundamental views. He repeatedly broke the usually even flow of his voice to indicate, with an emphatic gesture, that we had perhaps arrived at a critical, nay epochal, point marking the commencement of a new era of thought.
"Perhaps" was a word he never failed to emphasize. He persistently laid stress on his doubts, differentiated between hardened facts and hypotheses, still clinging to the hope that the new doctrine he was expounding would yet admit of an avenue leading back to the older views. This revolution, so he said, seemed to threaten things in science which a short while ago were looked upon as absolutely certain, namely, fundamental theorems of classical mechanics, for which we are indebted to the genius of Newton. For the present this revolution is of course only a threatening spectre, for it is quite possible that, sooner or later, the old established dynamical principles of Newton will emerge victoriously. Later in the course of his lecture he declared repeatedly that he felt a diffidence akin to fear at the sight of the accumulating number of hypotheses, and that it seemed to border on the impossible to attempt to arrange them into a system.
It is a matter of complete indifference how the revelations of Poincaré affected us individually ; if I may infer from my own case, there is only one word to express it --- staggering ! Oblivious of the doubts of the lecturer, I was swept along under the impetus of this new and mighty current of thought. This awakened two wishes in me : to become acquainted with Einstein's researches as far as lay within my power, and, if possible, to see him once in person. In me the abstract had become inseparable from the concrete personal element. The presentiment of the happy moment in the future hovered before my vision, whispering that I should hear his doctrine from his own lips.

Einstein in Berlin ca. 1915. [Photo from NASA website]
Several years later Einstein was appointed professor of the Academy of Sciences with the right of lecturing at the University of Berlin. This brought my personal wish within reach. Trusting to good fortune, I set about materializing it. In conjunction with a colleague I wrote him a letter asking him to honour with his presence one of the informal evenings instituted by our Literary Society at the Hotel Bristol. Here he was my neighbour at table, and chatted with me for some hours.
Nowadays his appearance is known to every one through the innumerable photos which have appeared in the papers. At that time I had never seen his countenance before, and I became absorbed in studying his features, which struck me as being those of a kindly, artistically inclined, being, in nowise suggesting a professor. He seemed vivacious and unrestrained in conversation, and, in response to our request, willingly touched upon his own subject as far as the place and occasion allowed, exemplifying Horace's saying, "Omne tulit punctum, qui miscuit utile dulci, tironem delectando pariterque monendo." It was certainly most delightful. Yet at moments I was reminded of a male sphinx, suggested by his highly expressive enigmatic forehead. Even now, after a warm acquaintanceship stretching over years, I cannot shake off this impression. It often overcomes me in the midst of a pleasant conversation interspersed with jests whilst enjoying a cigar after tea ; I suddenly feel the mysterious sway of a subtle intellect which captivates and yet baffles the mind.
Hotel Bristol, Unter den Linden, 1910.
At that time, early in 1916, only a few members of the Literary Society divined who it was that was enjoying their hospitality. In the eyes of Berlin, Einstein's star was beginning its upward course, but was still too near the horizon to be visible generally. My own vision, sharpened by the French lecture and by a friend who was a physicist, anticipated events, and already saw Einstein's star at its zenith, although I was not even aware at that time that Poincaré had in the meantime overcome his doubts and had fully recognized the lasting importance of Einstein's researches. ( Dr. Fritz Reiche, since that time a Dozent at the University, had repeatedly lent me his valuable aid in the study of technical writings by and about Einstein.) I had the instinctive feeling that I was sitting next to a Galilei. The fanfares sounded in the following years as a sign of appreciation by his contemporaries were only a fuller instrumentation of the music of destiny which had vibrated in my ears ever since that time.
I recollect one little incident : one of these lovers of literature, who was, however, totally ignorant of natural science, had accidentally seen several learned articles dealing with Einstein's Reports for the Academy, and had preserved the cuttings in his pocket-book. He considered this a fitting opportunity for enlightenment. Surely a brief question would suffice to guide one through these intricate channels. "Professor, will you kindly tell me the meaning of potential, invariant, contravariant, energy-tensor, scalar, relativity-postulate, hyper-Euclidean, and inertial system ? Can you explain them to me in a few words ?"
"Certainly," said Einstein, "those are merely technical expressions !"
That was the end of the little lesson.
Far into the night three of us sat in a café while Einstein gently lifted the veil from his newest discovery for the benefit of my journalist friend and myself. We gathered from his remarks that a Special Theory of Relativity formed a prelude to a general theory which embraced the problem of gravitation in its widest sense, and hence also the physical constitution of the world. What interested me apart from this theme, which was, of course, only touched upon lightly, was the personal question in its psychological aspect.
"Professor," said I, "such investigations must involve enormous mental excitement. I imagine that there lurks behind every solved problem ever and again some new problem with a threatening or a fascinating aspect, as the case may be, each one calling up a tumult of emotion in its author. How do you succeed in mastering this difficulty ? Are you not continually tormented by restless thoughts that noisily invade your dreams ? Do you ever succeed at all in enjoying undisturbed slumber ?"
The very tone in which the answer was given showed clearly how free he felt himself of such nervous troubles which usually oppress even the mediocre thinker. It is fortunate that such affections do not penetrate to his high level. "I break off whenever I wish," he said, "and banish all difficulties when the hour for sleep arrives. Thinking during dreams, as in the case of artists, such as poets and composers, by which they weave the thread of day on into the night, is quite foreign to me. Nevertheless, I must confess that at the very beginning, when the special theory of relativity began to germinate in me, I was visited by all sorts of nervous conflicts. When young I used to go away for weeks in a state of confusion, as one who at that time had yet to overcome the stage of stupefaction in his first encounter with such questions. Things have changed since then, and I can assure you that there is no need to worry about my rest."
"Notwithstanding," I answered, "cases may arise in which a certain result is to be verified by observation and experiment. This might easily give rise to nerve-racking experiences. If, for instance, a theory leads to a calculation which does not agree with reality, the propounder must surely feel considerably oppressed by this mere possibility. Let us take a particular event. I have heard that you have made a new calculation of the path of the planet Mercury on the basis of your doctrine. This must certainly have been a laborious and involved piece of work. You were firmly convinced of the theory, perhaps you alone. It had not yet been verified by an actual fact. In such cases conditions of great psychological tension must surely assert themselves. What in Heaven's name will happen if the expected result does not appear ? What if it contradicts the theory ? The effect on the founder of the theory cannot even be imagined !"
"Such questions," said Einstein, "did not lie in my path. That result could not be otherwise than right. I was only concerned in putting the result into a lucid form. I did not for one second doubt that it would agree with observation. There was no sense in getting excited about what was self-evident."
Let us now consider several facts of natural science, apart from this chat, but suggested by it, which caused Einstein little excitement, but the whole world generally, so much the more. By way of illustration we shall link them up with the result of a forerunner who, like Einstein, fixed on paper what should happen in the heavens.

Urbain Leverrier
Formerly, whenever one wished to play a particularly effective trump card in favour of research work it was customary to quote the achievement of the French astronomer Leverrier who, pen in hand, established the material existence of a planet at that time quite unknown and unnoticed. Certain disturbances in the orbit of the planet Uranus, which was regarded as being the most distant of the wandering stars, at that time had caused him to believe in the certainty of the existence of a still more distant planet, and by using merely the theoretical methods of celestial mechanics in connexion with the problem of three bodies he succeeded in revealing what was hidden behind the visible constellations. He reported the result of his calculations to the Berlin Observatory about seventy-five years ago, as it was at that time in possession of the best instruments. It was then that the amazing event happened : on the very same evening an observer in Berlin, Gottfried Galle, discovered the predicted new star almost exactly at the point of the heavens for which it was prophesied, only half the moon's diameter from it. The new planet Neptune, the farthest outpost of our solar system, reposed as a prisoner in his telescope ; the seemingly undiscoverable star had capitulated in the face of mental efforts of a mathematical scholar, who, in reasoning meditation, had sketched his curves in the quiet atmosphere of his study.
This was certainly bewildering enough, but nevertheless this incredible result which stirred the imagination so strongly was directly rooted in reality, lay on the path of research, followed of necessity from the laws of motion known at that time, and disclosed itself as a new proof of the doctrines of astronomy which had long been recognized as supreme and incontestable. Leverrier had not created these, but had found them ready ; he applied them with the mind of genius. Anyone who nowadays is sufficiently trained to work through the highly complicated calculation of Leverrier has every reason to marvel at a work which is entirely mathematical throughout.
Graphic by R. J. Hall, whose caption reads: "This illustration shows two planets orbiting about a common star. The outer planet takes more time to complete an orbit than the inner planet, so once per orbit the inner planet overtakes the outer planet. When the planets are at a, the outer planet exerts a gravitational perturbation that accelerates the inner planet, advancing the body ahead of its normal path. When the planets reach b, the reverse is true and the inner planet is decelarated. This perturbing influence is what led to the discovery of the planet Neptune."
Our own times have been marked by an event of still greater significance.
Irregularities had shown themselves in observation of the heavens that could not be explained or grasped by the accepted methods of classical mechanics. To interpret them, ideas of a revolutionary nature were necessary. Man's view of the plan according to which the universe is mapped out had to be radically reformed to bring within comprehension the problems that presented themselves in macroscopic as well as in microscopic regions, in the courses of the stars as well as in the motions of the ultimate constituents of the atom of material bodies, incapable of being directly observed. The goal consisted in bringing those doctrines in which truth had been proclaimed in its essential features, but not exhaustively, by the genius of Copernicus, Galilei, Kepler, and Newton, to their conclusion by penetrating as far as possible into the mysteries of the structure of the universe. This is where Einstein comes forward.
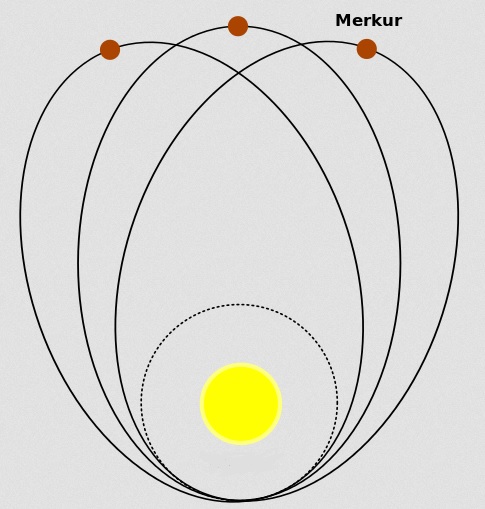
Drawing by D. Henry and others.
Whereas the outermost planet Neptune had bowed to the accepted laws, by merely disclosing his presence, Mercury, the innermost planet, preserved an obstinate attitude even in the face of the most refined calculations. These always led to an unaccountable remainder, a disagreement, which seemed very small when expressed in numbers and words, and yet enclosed a deep secret. Wherein did this disagreement consist ? In a difference of arc which had likewise been discovered by Leverrier and which defied explanation. It was only a matter of about forty-five insignificant quantities, seconds of arc, which seemed vanishingly small since this deviation did not occur within a month or a year, but was spread over a whole century. By just so much, or rather so little, the rotation of Mercury's orbit differed from what might be termed the allowable astronomical value. Observation was exact, calculation was exact ; why, then, the discrepancy ?
It was thus inferred that there was still some hidden unexplored factor which had to be taken into account in the fundamental principles of celestial mechanics. The formerly invisible Neptune confirmed the old rule by appearing. Mercury, which was visible, opposed the rule.
In 1910 Poincaré had touched upon this embarrassing question, mentioning that here was a possibility of testing the new mechanics.
He declined the suggestion of some astronomers that this was again a Leverrier problem and that there must exist another undiscovered planet still nearer the sun and disturbing Mercury's orbit. He also refused to accept the assumption that the disturbance might be caused by a ring of cosmic matter distributed round the sun. Poincaré divined that the new mechanics could supply the key to the enigma, but, obviously to be quite conscientious, he expressed his presentiment in very cautious terms. On that occasion he said that some special cause had yet to be found to explain the anomaly of Mercury's behaviour ; till that was discovered one could only say that the new doctrine could not be regarded as in contradiction to astronomical facts. But the true explanation was gradually drawing near.
Five years later, on 18th November 1915, Albert Einstein presented to the Prussian Academy of Sciences a paper which solved this riddle which, expressed in seconds, seemed so insignificant and yet was of such enormous importance in its bearing on fundamental questions. He proved the problem was solved quite accurately if the general Theory of Relativity he had founded was accepted as the only valid basis for the phenomena of cosmic motions.
Many would at this point express a wish to have the essence of the doctrine of relativity explained in an easily intelligible manner. Indeed, some would go even further in their desire, and would ask for a simple description in a few succinct sentences. This, measured in terms of difficulty and possibility, would be about equivalent to wishing to learn the history of the world by reading several quarto pages of manuscript or a novelette. But even if we start at long range and use elaborate materials for our description, we should have to give up the idea that this knowledge may be gained with playful ease. For this doctrine, inasmuch as it discloses the relationship between mathematical and physical events, emerges out of mathematics, which thus limits the mode of its representation. Whoever undertakes to present it in a form in which it is easily intelligible, that is quite unmathematical and yet complete, is engaged in an impossible venture ; he is like one who would whistle Kepler's Laws on the flute or would elucidate Kant's Critique of Pure Reason by means of coloured illustrations. In all frankness we must confess once and for all that whenever popular accounts are attempted they can be only in the nature of vague suggestions removed from the domain of mathematics. But even such indications have a fruitful result if they succeed in focusing the attention of the reader or the hearer so that the connexions, the Haupt-Leitmotive, so to speak, of the doctrine, are at least suggested.
It must therefore suffice if we place the conception of approximation in the foreground here as in other parts of this book. Till quite recently Newton's Equations of Motion were used as a foundation for verifying astronomical occurrences. These are symbolical representations expressed as formulæ that contain in an exceedingly simple form the law of mass attraction. They express the comprehensive principle that the attraction is directly proportional to the mass and inversely proportional to the square of the distance ; so that the moving force is doubled when the mass is doubled, whereas if the distance is double, the force is only a quarter as great, if the distance is trebled, the force becomes one-ninth as great.
According to the Theory of Relativity this fundamental law is not wrong or invalid, but no longer holds fully if pursued to its last inferences. In applying corrections to it, new factors occur, such as the ratio of given velocities to the velocity of light, and the new geometry which operates with "world-lines" in space which, amalgamated with the dimension of time, is regarded as a quadruply extended continuum.
Einstein has actually supplemented these fundamental equations for the motion of masses so that the original form states the true condition of affairs only approximately, whereas Einstein's equations give the motion with very great accuracy.
The above-mentioned essay of Einstein is carried out as if the structure bequeathed to us by Newton required the addition of a final, very delicate pinnacle. For the mathematician this pinnacle is given as a combination of signs, representing a so-called "Elliptic Integral" [correcting the published English translation, which twice in this paragraph has "interval" for "integral" -- possibly a typesetter's error, since the German reads Integral.]. Such an integral is a very weird construction, and the man who will make it apprehended by the general reader is yet to be born. When Lord Byron (in the Dedication to Don Juan) spoke of Coleridge
Explaining Metaphysics to the nation ---
I wish he would explain his Explanation !
he had still a sure footing in intelligibility, compared with the non-mathematician, who demands an explanation for such a construction. And what a complex of mathematical dangers must be overcome even before the question of the meaning of this integral is crystallized out !

Precession of an elliptical orbit. Watch the perihelion advance. [Animation by "WillowW"]
But now the explanation had arrived and could be evaluated, if only approximately. Before we give the result, let us just describe at least one technical term, namely, "Perihelion". It is that point of a planetary orbit which lies nearest the sun. This orbit is an ellipse, that is, an elongated curved line in the interior of which one distinguishes a major axis in the direction of elongation, and a minor axis perpendicular to the former at its middle point. The perihelion of a planetary orbit is at one of the end points of the major axis.
In time the perihelion alters its position in space, advancing in the same sense as the orbit is traversed. It would naturally be assumed that the amount of this advance as measured astronomically would agree with the calculation resulting from Newton's theory. But this was not the case. An unaccountable remainder was left over, which astronomers ascertained to be 45 seconds (of arc) per 100 years, with a possible fluctuation of plus or minus 5 seconds. Thus, if the new result were found to lie between 40 and 50 seconds, the new theory would henceforth have to be regarded as the only valid one.
It happened just as Einstein predicted : calculation according to his theory shows that for the planet Mercury the perihelion should advance 43 seconds per 100 years. This signifies full agreement with observation and fully removes the former apparent difficulty. Whereas Leverrier in his time had pointed out a new planet, Einstein brought to view something far more important : a new truth.
It was a test of accuracy so dazzling that it alone would have sufficed to prove the correctness of Einstein's Principles. Yet, a second test, fraught with graver and more far-reaching consequences, presented itself -- a test which could be applied only several years later, and which developed into a scientific event of the highest importance.
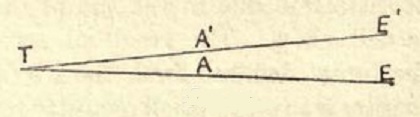
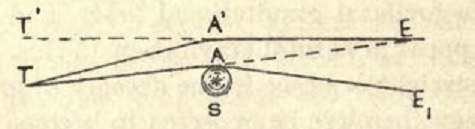
"A star at T sends out rays in straight lines in all directions. One of these, TAE, strikes the earth E and renders the star visible ; other rays such as TAE′ miss the earth. Now interpose the sun S near the paths of the rays. The effect is to bend the ray TA towards the sun into the direction AE1 so that it now misses the earth. The ray which reaches the earth is the ray TA′, which is now bent in the direction A′E. Thus the star is now seen at T′ on EA′ produced, instead of on ET as before, and the effect of the sun has been to displace its apparent position outwards."
From An Introduction to the Theory of Relativity by L. Bolton [London: Methuen, 1921].
For at the same time that Einstein solved the problem of Mercury, he had investigated the path of light-rays according to his revolutionary method, and had arrived at the conclusion that every ray under the influence of a gravitational field, as, for example, in the neighbourhood of the sun, must become curved. This daring announcement gave a new possibility of putting the theory to a practical test during the total echpse of the sun on 29th May 1919. For, when the disc of the sun is obscured, the stars that are closest to it become visible (even to the naked eye). They may be photographed, and the distances of the points of light on the negative allow us to detect whether the rays from the stars in passing the massive body of the sun have actually been deflected by the amount prophesied by Einstein.
Once again current thought encountered a sharp corner, and "common sense", which furnishes its own certificate of merit, threatened to become rebellious. How now ? A ray from a star could be curved ? Does not this contradict the elementary conception of the straight lines, that is, the shortest lines, for which we have no better picture than just these rays ? Did not Leonardo da Vinci define the straight line by means of the term linea radiosa ?
But such supposedly self-evident facts have no longer a place in the space-time world. The point was to test whether a physical anomaly which had been predicted actually existed. If the deflection of the rays really happened, it should manifest itself in the distances between the stars on the photographic plate being greater than one would expect from their actual position.
For the curvature has its concave side towards the sun, as is easy to see, once the phenomenon is regarded as possible. It is as if the ray were directly subject to gravitation. Let us take two stars, one on each side of the sun. On account of the concavities the eye receives rays from them under a greater visual angle than if the rays were straight, and interprets this angle as denoting a greater distance between the sources of light, that is, it sees the two stars farther apart than in the case of rectilinear propagation.

Graphic: Cmglee, Wikipedia
By how much farther apart ? The preceding calculation and the subsequent direct observation demanded incredible delicacy of measurement. If we suppose the whole arc of the heavens divided into easily picturable units such as degrees, then the apparent width of the moon is about half a degree. We may still easily imagine the thirtieth part of this, namely, a minute of arc. But the sixtieth part of the latter, the second of arc, vanishes almost out of the range of sense-perception. And it was just this minute measure that came into question, for the theory which had been developed from pure thought predicted a deflection of one and seven-tenths seconds of arc. This corresponds to about a hairbreadth when seen at a distance of 17 yards, or to the thickness of a match at a distance of over half a mile. One of the greatest problems of the most comprehensive science depended on this unthinkably small measure.
In no sense did Einstein himself entertain a possibility of doubt. On repeated occasions before May 1919 I had opportunities of questioning him on this point. There was no shadow of a scruple, no ominous fears clouded his anticipations. Yet great things were at stake.
Observation was to show "the correctness of Einstein's world system" by a fact clearly intelligible to the whole world, one depending on a very sensitive test of less than two seconds of arc.
"But, Professor," said I, on various occasions, "what if it turns out to be more or less ? These things are dependent on apparatus that may be faulty, or on unforeseen imperfections of observation." A smile was Einstein's only answer, and this smile expressed his unshakeable faith in the instruments and the observers to whom this duty was to be entrusted.
Moreover, it is to be remarked that no great lengths of time were available for comfortable experimentation in taking this photographic record. For the greatest possible duration of a total eclipse of the sun viewed at a definite place amounts to less than eight minutes, so that there was no room for mishaps in this short space of time, nor must any intervening cloud appear. The kindly co-operation of the heavens was indispensable -- and was not refused. The sun, in this case the darkened sun, brought this fact to light.
Two English expeditions had been equipped for the special occasion of the eclipse -- one to proceed to Sobral and the other to the Island of Principe, off Portuguese Africa ; they were sent officially with equipment provided in the main by the time-honoured Royal Society. Considering the times, it was regarded as the first symptom of the revival of international science, a praiseworthy undertaking. A huge apparatus was set into motion for a purely scientific object with not the slightest relation to any purpose useful in practical life. It was a highly technical investigation whose real significance could be grasped by only very few minds.
Yet interest was excited in circles reaching far beyond that of the professional scientist. As the solar eclipse approached, the consciousness of amateurs became stirred with indefinite ideas of cosmic phenomena. And just as the navigator gazes at the Polar Star, so men directed their attention to the constellation of Einstein, which was not yet depicted in stellar maps, but, from which something uncomprehended, but undoubtedly very important, was to blaze forth.
In June it was announced that the star photographs had been successful in most cases, yet for weeks, nay for months, we had to exercise patience. For the photographs, although they required little time to be taken, took much longer to develop and, above all, to be measured ; in view of the order of smallness of the distances to be compared, this was a difficult and troublesome task, for the points of light on the plate did not answer immediately with Yes or No, but only after mechanical devices of extreme delicacy had been carefully applied.
At the end of September they proclaimed their message. It was in the affirmative, and this Yes out of far-distant transcendental regions called forth a resounding echo in the world of everyday life. Genuinely and truly the one and seven-tenths seconds of arc had come out, correct to the decimal point. These points representing ciphers, as it were, had chanted of the harmony of the spheres in their Pythagorean tongue. The transmission of this message seemed to be accompanied by the echoing words of Goethe's Ariel:
With a crash the Light draws near !
Pealing rays and trumpet-blazes, ---
Eye is blinded, ear amazes.
Never before had anything like this happened. A wave of amazement swept over the continents. Thousands of people who had never in their lives troubled about vibrations of light and gravitation were seized by this wave and carried on high, immersed in the wish for knowledge although incapable of grasping it. This much all understood, that from the quiet study of a scholar an illuminating gospel for exploring the universe had been irradiated.

From the New York Times, 1919 November 10.
During that time no name was quoted so often as that of this man. Everything sank away in face of this universal theme which had taken possession of humanity. The converse of educated people circled about this pole, could not escape from it, continually reverted to the same theme when pressed aside by necessity or accident. Newspapers entered on a chase for contributors who could furnish them with short or long, technical or non-technical, notices about Einstein's theory. In all nooks and corners social evenings of instruction sprang up, and wandering universities appeared with errant professors that led people out the three-dimensional misery of daily life into the more hospitable Elysian fields of four-dimensionality. Women lost sight of domestic worries and discussed co-ordinate systems, the principle of simultaneity, and negatively-charged electrons. All contemporary questions had gained a fixed centre from which threads could be spun to each. Relativity had become the sovereign password. In spite of some grotesque results that followed on this state of affairs, it could not fail to be recognized that we were watching symptoms of mental hunger not less imperative in its demands than bodily hunger, and it was no longer to be appeased by the former books by writers on popular science and by misguided idealists.
And whilst leaders of the people, statesmen, and ministers made vain efforts to steer in the fog, to arrive at results serviceable to the nation, the multitude found what was expedient for it, what was uplifting, what sounded like the distant hammering of reconstruction. Here was a man who had stretched his hands towards the stars ; to forget earthly pains one had but to immerse oneself in his doctrine. It was the first time for ages that a chord vibrated through the world invoking all eyes towards something which, like music or religion, lay outside political or material interests.
The mere thought that a living Copernicus was moving in our midst elevated our feelings. Whoever paid him homage had a sensation of soaring above Space and Time, and this homage was a happy augury in an epoch so bare of brightness as the present.
As already remarked, there was no lack of rare fruits among the newspaper articles, and a chronicler would doubtless have been able to make an attractive album of them. I brought Einstein several foreign papers with large illustrations which must certainly have cost the authors and publishers much effort and money. Among others there were full-page beautifully coloured pictures intended to give the reader an idea of the paths pursued by the rays from the stars during the total eclipse of the sun. These afforded Einstein much amusement, namely, e contrario, for from the physical point of view these pages contained utter nonsense. They showed the exact opposite of the actual course of the rays inasmuch as the author of the diagrams had turned the convex side of the deflected ray towards the sun. He had not even a vague idea of the character of the deflection, for his rays proceeded in a straight line through the universe until they reached the sun, where they underwent a sudden change of direction reminiscent of a stork's legs.
The din of journalistic homage was not unmixed with scattered voices of dissent, even of hostility. Einstein combated these not only without anger but with a certain satisfaction. For indeed the series of unbroken ovations became discomfiting, and his feelings took up arms against what seemed to be developing into a star-artist cult. It was like a breath of fresh air when some column of a chance newspaper was devoted to a polemic against his theory, no matter how unfounded or unreasoned it may have been, merely because a dissonant tone broke the unceasing chorus of praise. On one occasion he even said of a shrill disputant, "The man is quite right !" And these words were uttered in the most natural manner possible. One must know him personally if one is to understand these excesses of toleration. So did Socrates defend his opponents.
In our conversation we returned to the original question, and I asked whether there was no means of making the deflection of the ray intelligible to an average person.
Einstein replied : "In a very superficial manner this is certainly possible." And with a few strokes on the paper, which I shall here try to describe in words, he gave his explanation in terms something like the following :
Since Moszkowski does not attempt to reproduce Einstein's drawing of the famous thought experiment, we will use this one (by Markus Poessel). Readers of this blog may recall that Lewis Carroll had the same idea independently in 1889.
This square is to denote the cross-section of a closed box which we imagine to be situated somewhere in the universe. Inside it there lives a physicist who makes observations and draws inferences from them. In the course of time he perceives, what is familiar to all of us, that every body not supported and left to itself, for example, a stone that is released, drops to the floor with uniform acceleration, that is, with a steady increase of velocity in going downwards. There are two ways open to him to explain this phenomenon.
Firstly, he might suspect -- and this suspicion would be most likely to occur to him -- that his box was resting on some body in the heavens. For if indeed the box were a cave in some part of the world, the falling of the stone would suggest nothing unusual ; it would be quite self-evident to every occupant, and quite explicable to the physicist according to Galilei's (or Newton's) Laws for Falling Bodies. He need not necessarily restrict himself to the Earth, for if the box happened to be on some other star, this phenomenon of falling would likewise occur, with greater or less speed, and the body would certainly fall with uniform acceleration. Thus the physicist could say : "This is an effect of gravitation, exhibiting the property of weight which I explain to myself as usual, as due to the attraction of a heavenly body."
Secondly, another idea might strike him. For we stipulated nothing about the position of the box, and assumed only that it was to exist "somewhere in the universe." The physicist in the box might reason as follows :
"Supposing I am separted by incalculable distances from every attracting heavenly body, and supposing gravitation existed neither for me nor for the stone which I release from my hand, then it would still be possible for me to give a complete explanation of the phenomena I observe. I should only have to assume that the body is moving with uniform acceleration 'upwards.' The motion previously interpreted by me as a falling 'downwards' need not take place at all. The stone, as an inert body, could persist in its position (relative to the box or the observer), and would, in spite of this, show exactly the same behaviour when the box moves with acceleration upwards as if it were falling with increasing velocity downwards."
Now since our physicist has no system which might serve for reference and orientation, and since in his box which is shut off from the universe he has no means at his disposal of determining whether he is in the sphere of influence of an attracting heavenly body or not, both the above explanations are feasible for him and both are equally valid, and it is impossible for him to come to a decision in his choice. He can interpret the acceleration in either way, as being upwards or downwards, connected to one another by relativity ; a fundamental reason for preferring one interpretation to the other cannot be furnished, since the phenomenon of falling is represented unchanged whether he assumes the stone to be falling and the box to be at rest, or vice versa. This may be generalized in these words :
At every point of the world the observed acceleration of a body left to itself may be interpreted either as a gravitational or as an inertial effect -- that is, from the point of view of physics we may assert with equal right that the system (the box, the complex defining the orientation) from which I observe the event is accelerated, or that the event takes place in a gravitational field. The equal right to these two views is called the "Principle of Equivalence" by Einstein. It asserts the equivalence or the identity of inertial and gravitational mass.
If we familiarize ourselves with this identity, an exceedingly important road to knowledge is opened up to our consciousness. We arrive at the inevitable conclusion that every inertial effect that we perceive in bodies, the most essential quality of it, itself so to speak in its persistent nature, is to be traced back to the influence to which it is subjected by other bodies.
When this has become clear to us, we feel impelled to inquire how a ray of light would behave under the influence of gravitation. Hence we return to our physicist in the box, and we now know that as a consequence of the Principle of Equivalence we are free to assume either that an attracting heavenly body, such as the sun, is situated somewhere below the box, or to refer the phenomena to the box regarded as being accelerated upwards. In the box we distinguish the floor, the ceiling, four walls, and among these again, according to the position we take up, the wall on the left and its opposite one on the right.
We now imagine a marksman to be outside the box and having no connexion with us, being poised freely in space, and suppose him to fire out of a horizontal gun at the box so that the bullet pierces both the wall on the left and the wall on the right. Now, if everything else were to remain at rest, the holes in both walls would be equally distant from the floor, and the bullet would move in a straight line parallel to the floor and to the ceiling. But, as we have seen, all events happen as if the box itself moved with constant acceleration. The bullet that requires time to pass from one wall to the other thus finds that when it reaches the wall on the right the latter has advanced a little, so that the resulting hole is a little lower than that on the left wall. This means that the flight of the bullet, according to our observation in the interior of the box, is no longer rectilinear. In fact, if we trace the bullet from point to point, we should find that for us, situated in the box, it would describe a line bent downwards, with its concave side to the floor.
Exactly the same thing happens with a ray of light which is emitted by a source outside in a horizontal direction and which traverses the space between the walls (supposed transparent). Only the velocity would be different. In the course of its flight the ray would move like a projectile that is whizzing along at the rate of 180,000 miles per second. But provided sufficiently delicate means of measurement are applied, it should still be possible to prove the existence of an infinitesimal deflection from the rectilinear horizontal path, an insignificant concavity towards the floor.
Consequently this curvature of the light-ray (say, from a star) must also be perceptible in places where it is subject to the influence of a gravitational field. If we drop our imaginary picture of the box, the argument is in nowise altered. A ray from a star which passes close by the sun seems to our perception to be bent in towards the sun, and the order of this deflection can be determined if sufficiently delicate instruments be used. As above remarked, it is a question of detecting a difference of 1·7 seconds of arc, which is to be manifested as a distance on the photographic plate, and is actually found to be present.
The fact that scientists are able to detect this appears in itself a marvel of technical precision far in advance of "splitting hairs," for in comparison a single hair is, in this case, to be removed to a considerable distance if we are to use it to give an idea of the size of angle under consideration. Fortunately stellar photography has been developed so wonderfully that in every single case extraordinarily accurate results are got even from prehminary measurements.
In ordinary astronomical practice it is usually found that a millimetre in linear measure on the plate corresponds to a minute of arc. This means that the sun's disc itself has a diameter of 3 centimetres on the photograph. The stars appear as tiny dots, which may be sharply differentiated in an enlargement. Stars of the fourteenth order of magnitude and beyond it become visible, whereas the naked eye cannot see those of order higher than the sixth. A grating whose lines are an hundredth part of a millimetre wide is copied on to the plate to make the measurement more accurate, so that the positions of objects can be ascertained with certainty to within a few tenths of a second of arc. Thus the problem which was to be solved by the solar eclipse of 1919 lay within the realm of possibility as regards our means of measurement.

One of Eddington's eclipse negatives.
A copy of this photograph had been sent to Einstein from England, and he told me of it with evident pleasure. He continually reverted to the delightful little picture of the heavens, quite fascinated by the thing itself, without the slightest manifestation of a personal interest in his own success. Indeed, I may go further and am certainly not mistaken in saying his new mechanics did not even enter his head, nor the verification of it by the plate ; on the contrary, he displayed that disposition of the mind which in the case of genius as well as in that of children shows itself as naïveté. The prettiness of the photograph charmed him, and the thought that the heavens had been drawn up as for parade to be a model for it.
All things are repeated in the history of life. In these happenings, which mark the 29th May 1919 as a red-letter day in the history of science, we recognize a revival of the Sun Myth, unperceived by the individual, but as an expression of the universal consciousness, just as, when Copernicus converted the geocentric picture of the universe into a heliocentric one, the Sun Myth again sprang into life ; the symbolization of faith in the light-giving and heat-giving star. This time it has arisen, purified of all dross, scarcely perceptible to our senses, like an aureole spun about the sun by far-distant sources of light, in honour of a principle, and even if most of us do not yet know what a "system of reference" means, yet for many such a system has unconsciously evolved, a thought-system serving as a reference for the development of their knowledge when they thought or spoke of Einstein.