The Chain Rule - a More Formal Approach

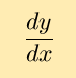
leads us to consider treating derivatives as fractions, so that given a composite function y(u(x)), we guess that

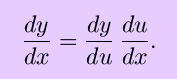
This speculation turns out to be correct, but we would like a better justification that what is perhaps a happenstance of notation. Let's start with the definition of the derivative and try to arrive at this result:

Given: y = f(u(x)).

By simple algebra, we know that

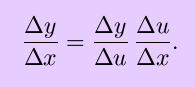
Then:

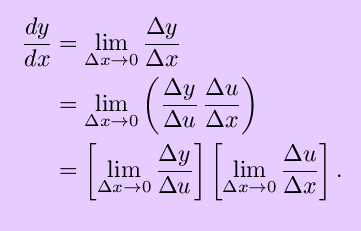
Differentiablility implies continuity; therefore

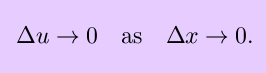
Then, we have

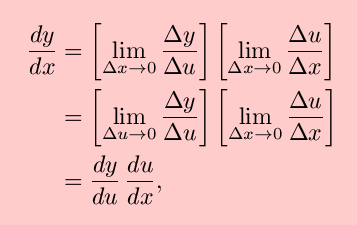
which is the Chain Rule.