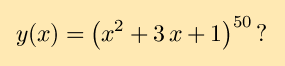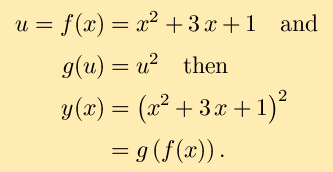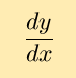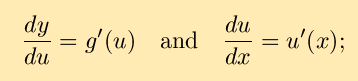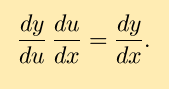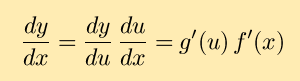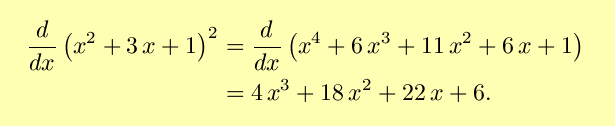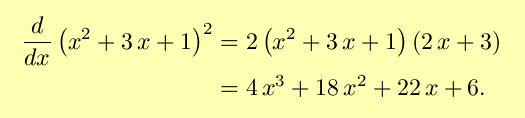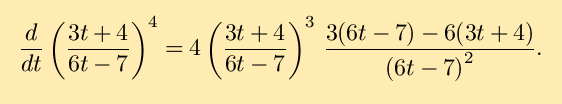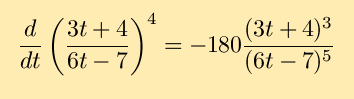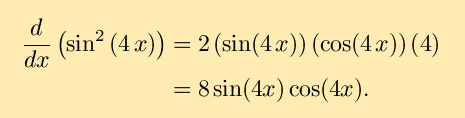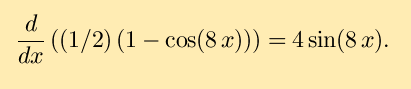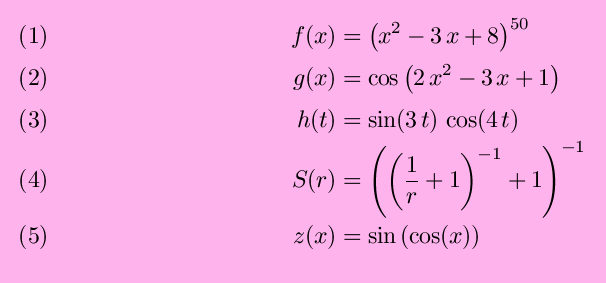The Chain Rule
The Chain Rule
Suggested Prerequesites:
The definition of the derivative
Suppose we want to find the derivative of
 We could hopefully multiply y(x) out and then
take the derivative with little difficulty (in fact, this will be done
below, as a check). But, what if, instead, the function were
We could hopefully multiply y(x) out and then
take the derivative with little difficulty (in fact, this will be done
below, as a check). But, what if, instead, the function were
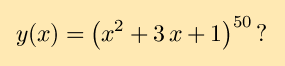 Would you want to apply the same method to this problem? Probably
not. Instead we need a method for dealing with composite functions,
functions which are one function applied to another. For example,
returning to the first y(x) above, if we let
Would you want to apply the same method to this problem? Probably
not. Instead we need a method for dealing with composite functions,
functions which are one function applied to another. For example,
returning to the first y(x) above, if we let
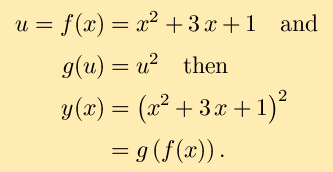 The function y(x) is the composite of
g with f.
The function y(x) is the composite of
g with f.
Our goal is to find the derivative
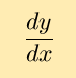 based on our knowledge of
the functions f and g. Now, we know that
based on our knowledge of
the functions f and g. Now, we know that
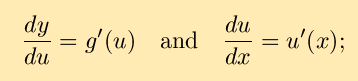 Leibniz's differential notation suggests that perhaps derivatives
can be treated as fractions, leading to the speculation that
Leibniz's differential notation suggests that perhaps derivatives
can be treated as fractions, leading to the speculation that
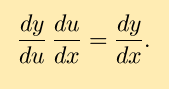 This leads to the (possible) chain rule:
This leads to the (possible) chain rule:
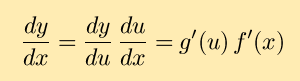 Let's apply this to our example and see if it works. First, we'll
multiply the product out and then take the derivative. Then we'll apply
the chain rule and see if the results match:
Let's apply this to our example and see if it works. First, we'll
multiply the product out and then take the derivative. Then we'll apply
the chain rule and see if the results match:
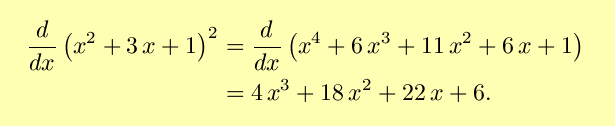 Using the chain rule as explained above,
Using the chain rule as explained above,
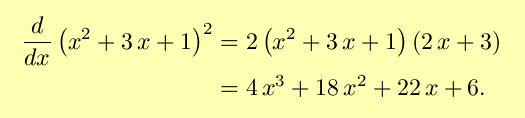 So, our rule checks out, at least for this example. It turns out that
this rule holds for all composite functions, and is invaluable for
taking derivatives. For a more rigorous proof, see The Chain Rule - a More Formal Approach.
So, our rule checks out, at least for this example. It turns out that
this rule holds for all composite functions, and is invaluable for
taking derivatives. For a more rigorous proof, see The Chain Rule - a More Formal Approach.
This rule is called the chain rule because we use it to take derivatives of
composties of functions by chaining together their derivatives. The
chain rule can be thought of as taking the derivative of the outer
function (applied to the inner function) and multiplying it times the
derivative of the inner function.
The chain rule is arguably the most important rule of differentiation.
It is commonly where most students tend to make mistakes, by forgetting
to apply the chain rule when it needs to be applied, or by applying it
improperly. Try to keep that in mind as you take derivatives.
Some examples:
- The function sin(2x) is the composite of the functions
sin(u) and u=2x. Then,

- An example that combines the chain rule and the quotient rule:
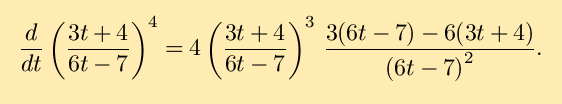 (The fact that this may be simplified to
(The fact that this may be simplified to
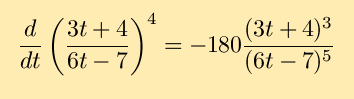 is more or less a happy coincidence unrelated to the chain rule.)
is more or less a happy coincidence unrelated to the chain rule.)
- The chain rule can be extended to composites of more than two
functions. For example sin2(4x) is a composite
of three functions; u2,
u=sin(v) and v=4x. Just remeber,
the derivative of the outer times the derivative of the inner times
... , giving
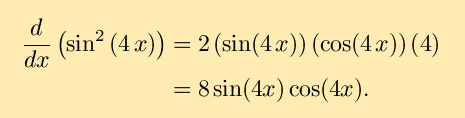 As a check, you may want to note that the above may be expressed as
As a check, you may want to note that the above may be expressed as
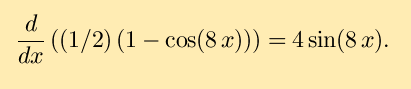
Exercises:
Differentiate the following with respect to the given independent variable:
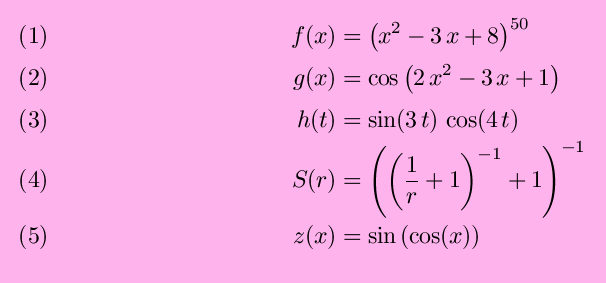
Solutions to the exercises |
Back to the Calculus page |
Back to the World Web Math top page
watko@mit.edu
Last modified August 28, 2007
 The Chain Rule
The Chain Rule The Chain Rule
The Chain Rule