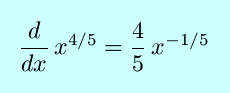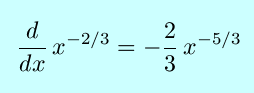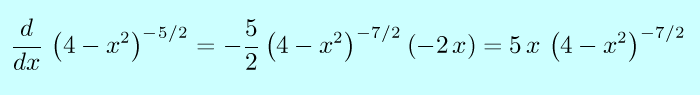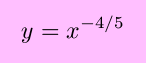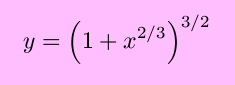Fractional Exponents

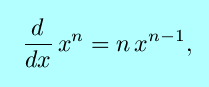
is valid for any integer exponent n. What about functions with fractional exponents, such as y = x^2/3? In this case, y may be expressed as an implicit function of x, y³ = x². Then,

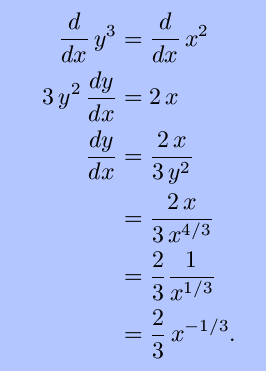
This is seen to be consistent with the Power Rule for n = 2/3.

Let's make a generalization of this example. Any rational number n can be expressed as p/q for some integers p and nonzero q. Then, for y = xⁿ,

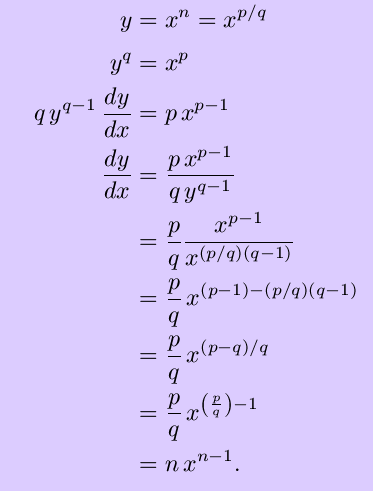
This is exactly what we would get if we assume the same power rule holds for fractional exponents as does for integral exponents. Note that we did not need to assume anything about the signs of p or q, other than the fact that q cannot be zero. Therefore, our power rule can now safely be applied to any rational exponents.

The definition of the derivative may also be used, but as the next two examples show, the direct use of the definition is often much more cumbersome than the improved Power Rule.

Consider the fairly simple case

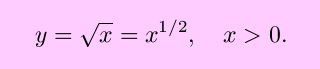
From the definition of the derivative,

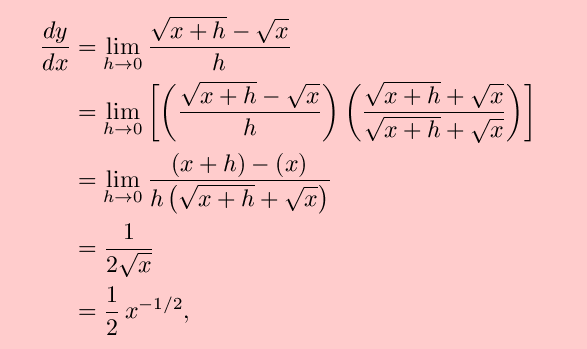
in agreement with the Power Rule for n = 1/2. For n = –1/2, the definition of the derivative gives

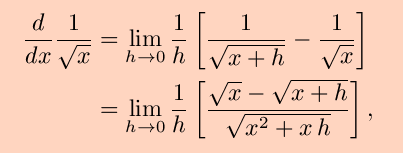
and a similar algebraic manipulation leads to

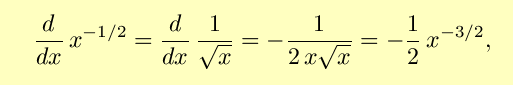
again in agreement with the Power Rule.

To see how more complicated cases could be handled, recall the example above,

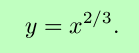
From the definition of the derivative,

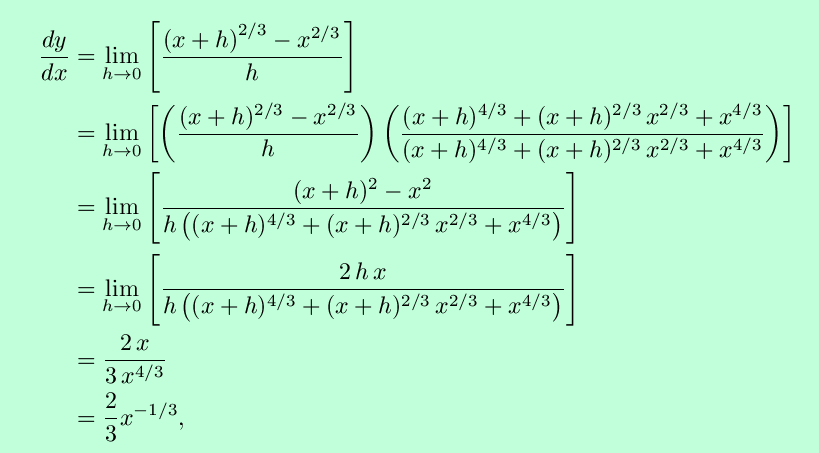
once more in agreement with the Power Rule. This example should clearly show that for fractional exponents, using the Power Rule is far more convenient than resort to the definition of the derivative.

Some examples:

Exercises:

Find the derivative with respect to x of each of the following functions.
1. 
   
   

2. 
   
   

3.