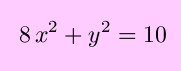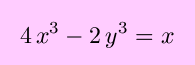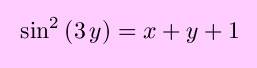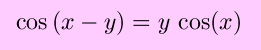Implicit Differentiation
Implicit Differentiation Implicit Differentiation
Implicit Differentiation
| There are two ways to define functions, implicitly and
explicitly. Most of the equations we have dealt with have
been explicit equations, such as
y = 2x-3, so that we can write
y = f(x) where
f(x) = 2x-3. But the
equation 2x-y = 3 describes the same
function. This second equation is an implicit definition of
y as a function of x. As there is no real
distinction between the appearance of x or y in
the second form, this equation is also an implicit definition of
x as a function of y
|
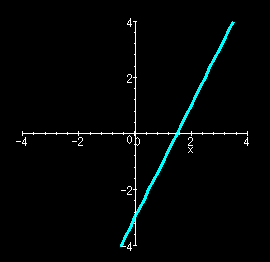
|
Not all implicit equations can be restated explicitly in a single equation. For example, the implicit equation x2+y2 = 9 needs two explicit equations,
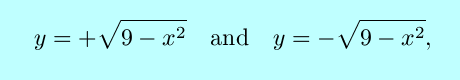
which are the top and bottom halves of a cricle respectively, to define the functional relation completely.
|
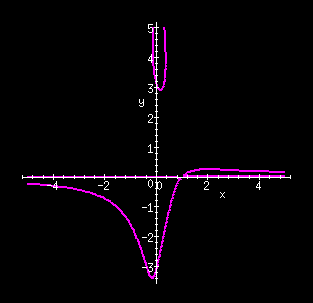
And xy = sin(y)+x2y2 (the magenta curves in the figure at the left) cannot be solved for either y as an explicit function of x or x as an explicit function of y. This implicit function is considered in Example 2. |
Perhaps surprisingly, we can take the derivative of implicit functions just as we take the derivative of explicit functions. We simply take the derivative of each side of the equation, remembering to treat the dependent variable as a function of the independent variable, apply the rules of differentiation, and solve for the derivative. Returning to our original example:
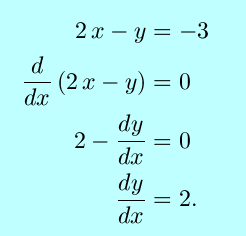
This is of course what we get from differentiating the explicit form,
y = 2x-3, with respect to x.
This simple example may not be very enlightening. Consider the second example, the equation that describes a circle of radius 3, centered at the origin. Taking the derivative of both sides with respect to x, using the power rule for the derivative of y,
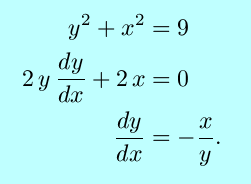
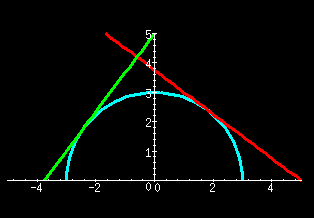
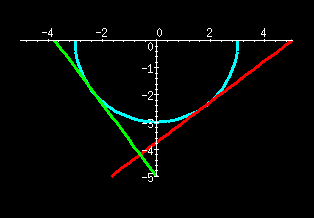
It can be seen from the figures that for either part of the circle, the slope of the tangent line has the opposite sign of the ratio x/y, and that the magnitude of the slope becomes larger as the tangent point nears the x-axis.
(For this case, finding dy/dx as an explicit function of x requires use of the power rule for fractional powers, usually considered later. This example may be thought of as a taste of things to come.)
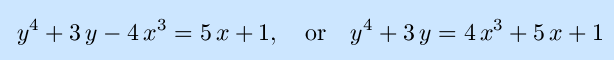
Note that this expression can be solved to give x as an explicit function of y by solving a cubic equation, and finding y as an explicit function of x would involve soving a quartic equation, neither of which is in our plan.
Using the chain rule and treating y as an implicit function of x,
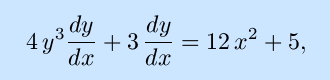
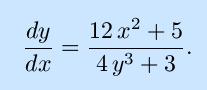
As in most cases that require implicit differentiation, the result in
in terms of both x and y. In general, if giving
the result in terms of x alone were possible, the original
expresson could be solved for y as an explicit function of
x, and implicit differentiation, while still correct, would
not be necessary.
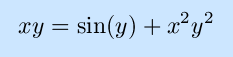
In this case, the chain rule and product rule are both used to advantage:
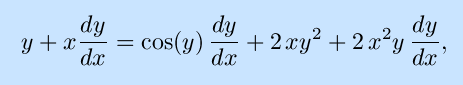
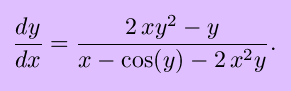
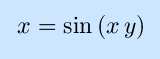 The use of inverse trigonometric functions allow this to be solve for y as an explicit function of x and graphed, as shown. However, this function serves as a good example of implicit differentiation: 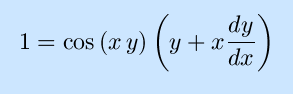
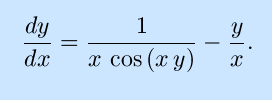
|
|