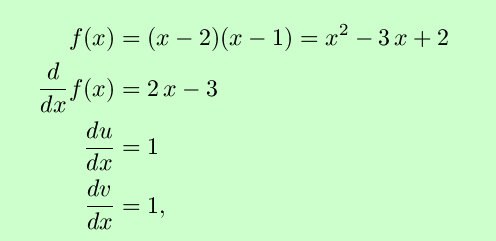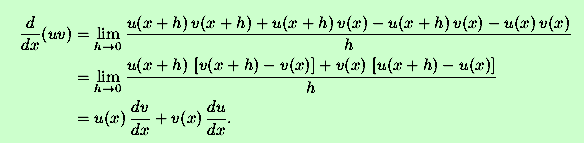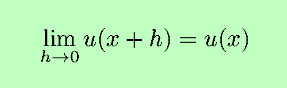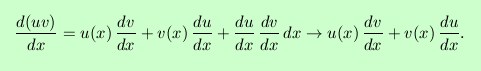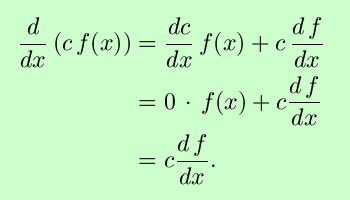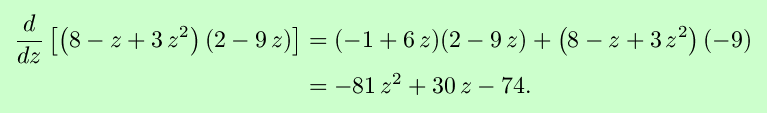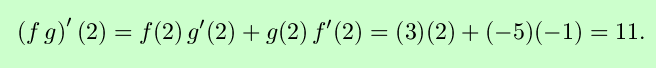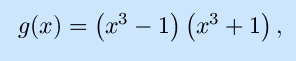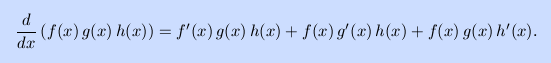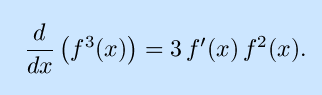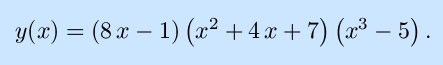The Product Rule

We'd like to be able to take the derivatives of products of functions whose derivatives we already know. For example f(x)=(x-2)(x-1) is a product of two functions, u(x)=x-2 and v(x)=x-1, both of whose derivatives we know to be 1. Wouldn't it be nice if the derivative of a product was the product of the derivative, as it is for sums? Unfortunately, this is not the case;

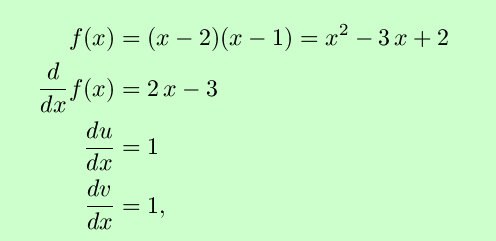
and in this quite simple case, it is easily seen that the derivative of a product is NOT the product of the derivatives. Although this naive guess wasn't right, we can still figure out what the derivative of a product must be. Remember: When intuition fails, apply the definition. Consider

Now we apply the trick of adding zero, in the form of u(x+h)v(x) -u(x+h)v(x) to the numerator, and after performing some minor algebra,

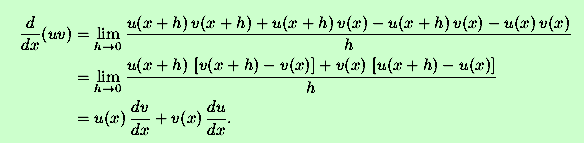In the last step,

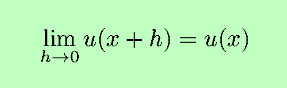because u(x) is differentiable at x and therefore ontinuous.

A good way to remember the product rule for differentiation is ``the first times the derivative of the second plus the second times the derivative of the first.'' It may seem non-intuitive now, but just see, and in a few days you'll be repeating it to yourself, too.

Another way to remember the above derivation is to think of the product u(x)v(x) as the area of a rectangle with width u(x) and height v(x). The change in area is d(uv), and is indicated is the figure below.

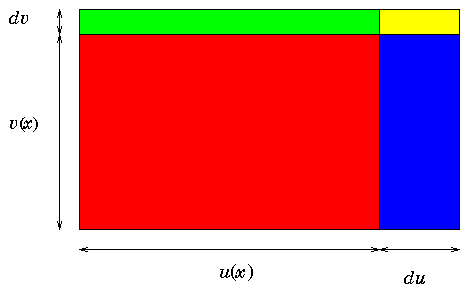As x changes, the area changes from the area of the red rectangle, u(x)v(x), to the area of the largest rectangle, the sum of the read, green, blue and yellow rectangles. The change in area is the sum of the areas of the green, blue and yellow rectangles,

In the limit of dx small, the area of the yellow rectangle is neglected. Algebraically,

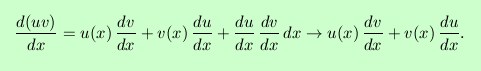``Neglecting'' the yellow rectangle is equivalent to invoking the continuity of u(x) above. This argument cannot constitute a rigourous proof, as it uses the differentials algebraically; rather, this is a geometric indication of why the product rule has the form it does.

Some examples:

  1. We can use the product rule to confirm the fact that the derivative of a constant times a function is the constant times the derivative of the function. For c a constant,

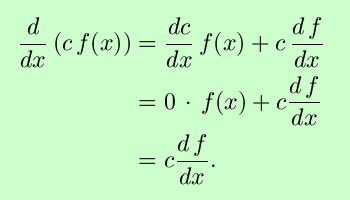
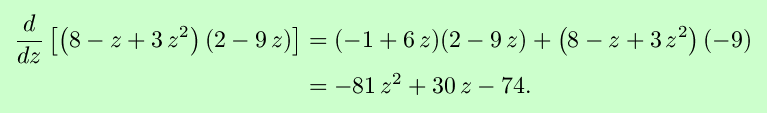
  2. Whether or not this is substantially easier than multiplying out the polynomial and differentiating directly is a matter of opinion; decide for yourself.

  3. If f and g are differentiable functions such that f(2)=3, f´(2)=-1, g(2)=-5 and g´(2)=2, then what is the value of (fg)´(2)?

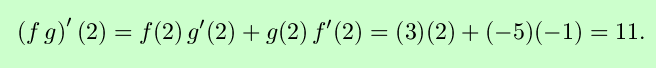
Exercises:

  1. With

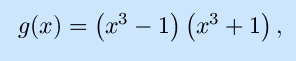
    what is g´(x)?

  2. If f, g and h are differentiable, use the product rule to show that

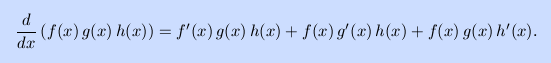    As a corollary, show that

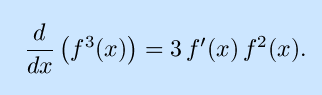    This is a special case of the chain rule.

  3. Find dy/dx where

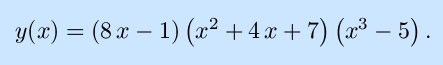
Solutions to the exercises | Back to the Calculus page | Back to the World Web Math top page
watko@mit.edu
Last modified February 11, 2003.