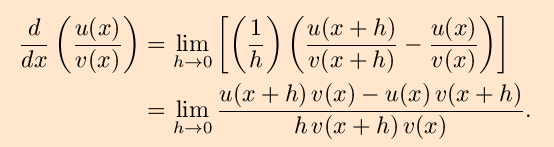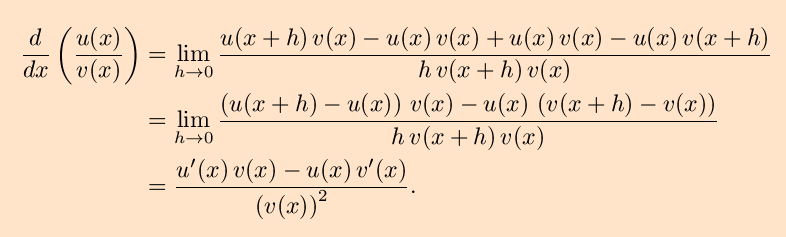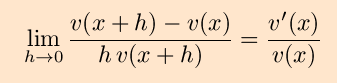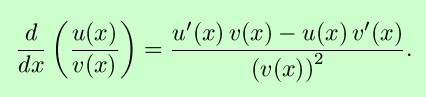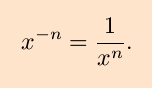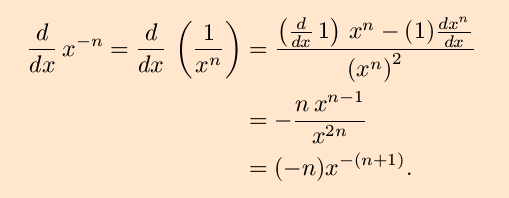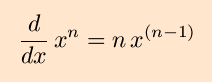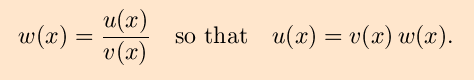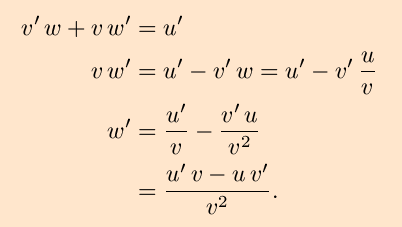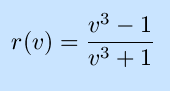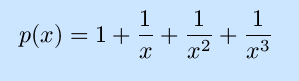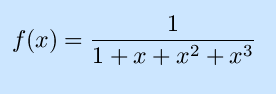The Quotient Rule
Suggested prerequestites:
Definition of the derivative,
The Product Rule
Now that we've seen how the derivative of a product is found, we can
extend the method to quotients. In fact, after the direct approach,
we'll show how the quotient rule may be obtained from the product rule
with only a little sleight of hand.
To begin the direct approach, we apply the definition
of the derivative to the ratio
u(x)/v(x) in order to find a
general formula;
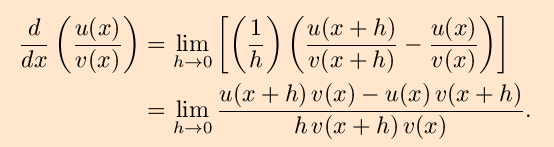We again use the trick of adding zero, this time in the form of
-u(x)v(x)
+u(x)v(x) to obtain
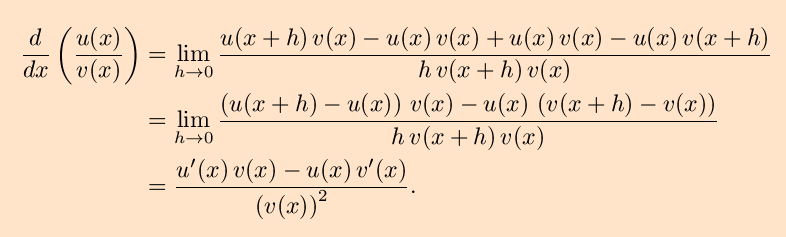So, the quotient rule for differentiation is ``the derivative of the
first times the second minus the first times the derivative of the
second over the second squared.'' Quite a mouthful but
still useful.
You might note that the above is far from rigorous, in that we
used
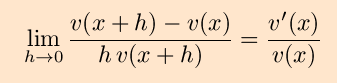and a similar limit for
u´(x)/v(x). However,
an implicit assumption in this derivation is that
v(x) is (a) non-zero at the points where the
derivative is evaluated and (b) differentiable, and hence continuous
at these points. In any event, the result
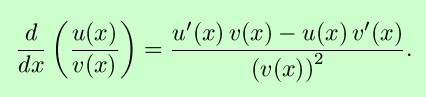is valid whenever u´(x) and
v(x) are differentiable and
v(x) is nonzero, and may be used with impunity.
We can use the quotient rule to find the derivative of
x-n where n is a positive integer, by
writing the expression instead as
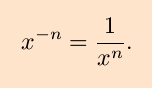Application of the quotient rule then gives
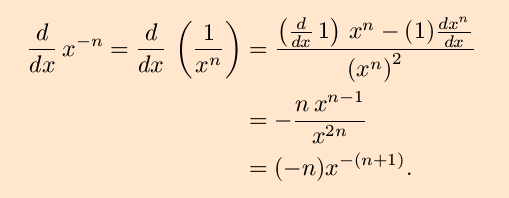This is what we would would have gotten by applying the power rule without considering the sign of
the power. By this, then, we know
that the power rule,
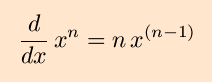can and should be extended to all integers.
To see how the quotient rule is obtained from the product rule, define
a function w(x) by
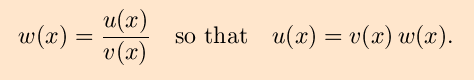Now, apply the product rule to u(x) (the
x-dependence will be supressed) and solve for
w´;
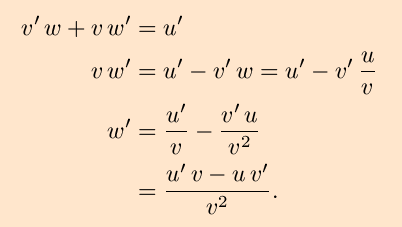
Exercises:
Find the derivatives of the following functions.
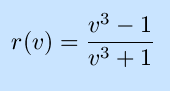
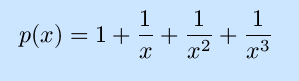
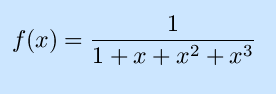
Solutions to the exercises |
Back to the Calculus page |
Back to the World Web Math top page
watko@mit.edu
Last modified August 29, 1998