- Heat transfer from, or to, a heat reservoir.
A heat reservoir (Figure 5.3) is a constant
temperature heat source or sink. Because the temperature is uniform,
there is no heat transfer across a finite temperature difference and
the heat exchange is reversible. From the definition of entropy (
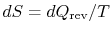 ),
),
where 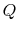 is the heat into the reservoir (defined here as
positive if heat flows into the reservoir.)
is the heat into the reservoir (defined here as
positive if heat flows into the reservoir.)
Figure 5.3:
Heat transfer from/to a heat
reservoir
|
|
- Heat transfer between two heat reservoirs
The entropy change of the two reservoirs in
Figure 5.4 is the sum of the entropy change of
each. If the high temperature reservoir is at 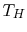 and the low
temperature reservoir is at
and the low
temperature reservoir is at 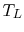 , the total entropy change is
, the total entropy change is
Figure 5.4:
Heat transfer between two
reservoirs
|
|
The second law says that the entropy change must be equal to or
greater than zero. This corresponds to the statement that heat must
flow from the higher temperature source to the lower temperature
source. This is one of the statements of the second law given in
Section 5.1.
Muddy Points
In the single reservoir example, why can the entropy decrease?
(MP 5.6)
Why does the entropy of a heat reservoir change if the temperature
stays the same? (MP 5.7)
How can the heat transfer from or to a heat reservoir be reversible?
(MP 5.8)
How can 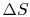 be less than zero in any process? Doesn't entropy
always increase? (MP 5.9)
be less than zero in any process? Doesn't entropy
always increase? (MP 5.9)
If
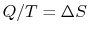 for a reservoir, could you add
for a reservoir, could you add 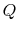 to any size
reservoir and still get the same
to any size
reservoir and still get the same 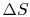 ?
(MP 5.10)
?
(MP 5.10)
- Possibility of obtaining work from a single heat reservoir
We can regard the process proposed in
Figure 5.5 as the absorption of heat, 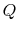 , by
a device or system, operating in a cycle, rejecting no heat, and
producing work. The total entropy change is the sum of the change in
the reservoir, the system or device, and the surroundings. The
entropy change of the reservoir is
, by
a device or system, operating in a cycle, rejecting no heat, and
producing work. The total entropy change is the sum of the change in
the reservoir, the system or device, and the surroundings. The
entropy change of the reservoir is
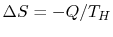 . The entropy
change of the device is zero, because we are considering a complete
cycle (return to initial state) and entropy is a function of state.
The surroundings receive work only so the entropy change of the
surroundings is zero. The total entropy change is
. The entropy
change of the device is zero, because we are considering a complete
cycle (return to initial state) and entropy is a function of state.
The surroundings receive work only so the entropy change of the
surroundings is zero. The total entropy change is
Figure 5.5:
Work from a single heat
reservoir
|
|
The total entropy change in the proposed process is thus less than
zero,
which is not possible. The second law thus tells us that we cannot
get work from a single reservoir only. The ``only'' is important; it
means without any other changes occurring. This is the other
statement of the second law we saw in Section 5.1.
Muddy Points
What is the difference between the isothermal expansion of a piston
and the (forbidden) production of work using a single reservoir?
(MP 5.11)
For the ``work from a single heat reservoir'' example, how do we
know there is no
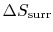 ?
(MP 5.12)
?
(MP 5.12)
How does a cycle produce zero 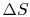 ? I thought that the whole
thing about cycles was an entropy that the designers try to
minimize. (MP 5.13)
? I thought that the whole
thing about cycles was an entropy that the designers try to
minimize. (MP 5.13)
- Entropy changes in the ``hot brick problem''
Figure 5.6:
The
``Hot Brick'' Problem
[Temperature equalization of two bricks]
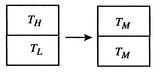
[Reservoirs used in reversible
state transformations]

|
We can examine in a more quantitative manner the changes that
occurred when we put the two bricks together, as depicted in
Figure 5.6(a). The process by which the two bricks
come to the same temperature is not a reversible one, so we need to
devise a reversible path. To do this imagine a large number of heat
reservoirs at varying temperatures spanning the range
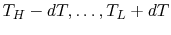 , as in Figure 5.6(b). The
bricks are put in contact with them sequentially to raise the
temperature of one and lower the temperature of the other in a
reversible manner. The heat exchange at any of these steps is
, as in Figure 5.6(b). The
bricks are put in contact with them sequentially to raise the
temperature of one and lower the temperature of the other in a
reversible manner. The heat exchange at any of these steps is 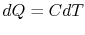 . For the high temperature brick, the entropy change is:
. For the high temperature brick, the entropy change is:
where 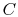 is the heat
capacity of the brick (J/kg). This quantity is less than zero. For
the cold brick,
is the heat
capacity of the brick (J/kg). This quantity is less than zero. For
the cold brick,
The entropy change of the
two bricks is
The process is not
reversible.
- Difference between the free expansion and the reversible
isothermal expansion of an ideal gas
The essential difference between the free expansion in an insulated
enclosure and the reversible isothermal expansion of an ideal gas
can also be captured clearly in terms of entropy changes. For a
state change from initial volume and temperature 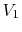 ,
, 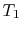 to
final volume and (the same) temperature
to
final volume and (the same) temperature 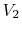 ,
, 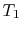 the entropy
change is
the entropy
change is
or, making use of the equation of state and the fact that 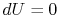 for an isothermal process,
for an isothermal process,
This is the entropy
change that occurs for the free expansion as well as for the
isothermal reversible expansion processes —- entropy changes are
state changes and the two system final and end states are the same
for both processes.
For the free expansion:
There is no change in the entropy of
the surroundings because there is no interaction between the system
and the surroundings. The total entropy change is therefore,
There are several points to note from this result:
-
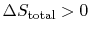 so the process is not
reversible.
so the process is not
reversible.
-
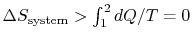 ;
the equality between
;
the equality between 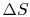 and
and 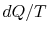 is only for a reversible
process.
is only for a reversible
process.
- There is a direct connection between the work needed
to restore the system to the original state and the entropy change:
The quantity 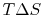 has a physical meaning as ``lost
work'' in the sense of work which we lost the opportunity to
utilize. We will make this connection stronger in
Chapter 6.
has a physical meaning as ``lost
work'' in the sense of work which we lost the opportunity to
utilize. We will make this connection stronger in
Chapter 6.
For the reversible isothermal expansion:
The entropy is a state variable so the entropy change of the system
is the same as before. In this case, however, heat is transferred to
the system from the surroundings (
 ) so
that
) so
that
The heat transferred from the surroundings, however, is equal to the
heat received by the system:
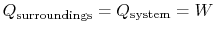 .
.
The total change in
entropy (system plus surroundings) is therefore
The
reversible process has zero total change in entropy.
On the example of free expansion versus isothermal expansion, how do
we know that the pressure and volume ratios are the same? We know
for each that  and
and 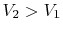 .
(MP 5.14)
.
(MP 5.14)


 [Reservoirs used in reversible
state transformations]
[Reservoirs used in reversible
state transformations]

![]() , as in Figure 5.6(b). The
bricks are put in contact with them sequentially to raise the
temperature of one and lower the temperature of the other in a
reversible manner. The heat exchange at any of these steps is
, as in Figure 5.6(b). The
bricks are put in contact with them sequentially to raise the
temperature of one and lower the temperature of the other in a
reversible manner. The heat exchange at any of these steps is ![]() . For the high temperature brick, the entropy change is:
. For the high temperature brick, the entropy change is:
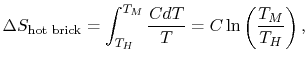
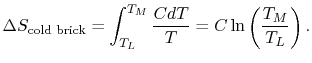
![$\displaystyle \Delta S_\textrm{bricks}=C\left[\ln\left(\frac{T_M}{T_H}\right)+\ln\left(\frac{T_M}{T_L}\right)\right]=
C\ln\left(\frac{T_M^2}{T_H T_L}\right)>0.$](img592.png)
![]() ,
, ![]() to
final volume and (the same) temperature
to
final volume and (the same) temperature ![]() ,
, ![]() the entropy
change is
the entropy
change is
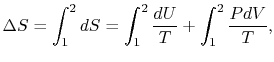
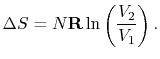
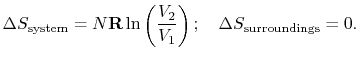

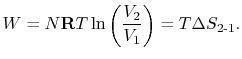
![]() ) so
that
) so
that
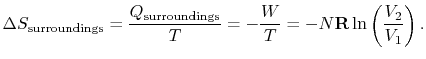

![]() and
and ![]() .
(MP 5.14)
.
(MP 5.14)
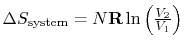 come from?
(MP 5.15)
come from?
(MP 5.15)