5.4 Entropy Changes in an Ideal Gas
[VW, S & B: 6.5- 6.6, 7.1]
Many aerospace applications involve flow of gases (e.g., air) and we
thus examine the entropy relations for ideal gas behavior. The
starting point is form (a) of the combined first and second law,
For an ideal gas,
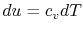 . Thus
. Thus
Using the equation of state for an ideal gas (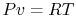 ), we can
write the entropy change as an expression with only exact
differentials:
), we can
write the entropy change as an expression with only exact
differentials:
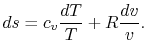 |
(5..2) |
We can think of Equation (5.2) as relating
the fractional change in temperature to the fractional change of
volume, with scale factors 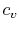 and
and 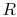 ; if the volume increases
without a proportionate decrease in temperature (as in the case of
an adiabatic free expansion), then
; if the volume increases
without a proportionate decrease in temperature (as in the case of
an adiabatic free expansion), then 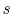 increases. Integrating
Equation (5.2) between two states ``1'' and
``2'':
increases. Integrating
Equation (5.2) between two states ``1'' and
``2'':
For a perfect gas with constant specific heats
In non-dimensional form (using
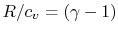 )
)
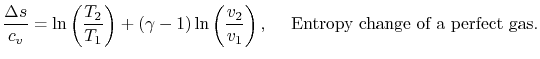 |
(5..3) |
Equation 5.3 is in terms of specific quantities. For
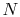 moles of gas,
moles of gas,
This expression gives entropy change in terms of temperature and
volume. We can develop an alternative form in terms of pressure and
volume, which allows us to examine an assumption we have used. The
ideal gas equation of state can be written as
Taking differentials of both sides yields
Using the above equation in Eq. (5.2), and
making use of the relations
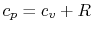 ;
;
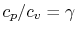 , we
find
, we
find
or
Integrating between two states 1 and 2
![$\displaystyle \frac{\Delta s}{c_v}=\ln\left(\frac{P_2}{P_1}\right)+\gamma\ln\le...
...v_1}\right) =ln\left[\frac{P_2}{P_1}\left(\frac{v_2}{v_1}\right)^\gamma\right].$](img575.png) |
(5..4) |
Using both sides of (5.4) as exponents we obtain
![$\displaystyle \frac{P_2v_2^\gamma}{P_1 v_1^\gamma}=\left[Pv^\gamma\right]^2_1=e^{\Delta s/c_v}.$](img576.png) |
(5..5) |
Equation (5.5) describes a general process.
For the specific situation in which
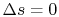 , i.e., the entropy
is constant, we recover the expression
, i.e., the entropy
is constant, we recover the expression
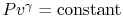 . It was stated that this expression applied to a
reversible, adiabatic process. We now see, through use of the second
law, a deeper meaning to the expression, and to the concept of a
reversible adiabatic process, in that both are characteristics of a
constant entropy, or isentropic, process.
. It was stated that this expression applied to a
reversible, adiabatic process. We now see, through use of the second
law, a deeper meaning to the expression, and to the concept of a
reversible adiabatic process, in that both are characteristics of a
constant entropy, or isentropic, process.
Muddy Points
Why do you rewrite the entropy change in terms of 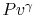 ?
(MP 5.4)
?
(MP 5.4)
What is the difference between isentropic and adiabatic?
(MP 5.5)
Douglas Quattrochi
2006-08-06
| 
