5.3 Combined First and Second Law Expressions
The first law, written in a form that is always true:
For reversible processes only, work or heat may be rewritten
as
Substitution leads to other forms of the first law true for
reversible processes only:
(If the substance has other work modes, e.g., stress, strain,
where 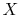 is a pressure-like quantity, and
is a pressure-like quantity, and 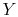 is a volume-like
quantity.)
is a volume-like
quantity.)
Substituting for both 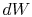 and
and 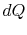 in terms of state variables,
in terms of state variables,
The above is always true because it is a relation between properties
and is now independent of process.
In terms of specific quantities:
The combined first and second law expressions are often more
usefully written in terms of the enthalpy, or specific enthalpy,
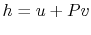 ,
,
Or, since
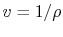 ,
,
In terms of enthalpy (rather than specific enthalpy) the relation is
Douglas Quattrochi
2006-08-06
|

