- Entropy as defined from a microscopic point of view is a measure
of randomness in a system.
- The entropy is related to the
probabilities
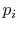 of the individual quantum states of the system
by
of the individual quantum states of the system
by
where 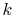 , the Boltzmann constant, is given by
, the Boltzmann constant, is given by
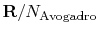 .
.
- For a system in which there are
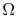 quantum states,
all of which are equally probable (for which the probability is
quantum states,
all of which are equally probable (for which the probability is
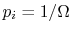 ), the entropy is given by
), the entropy is given by
The more quantum states, the more the randomness and uncertainty
that a system is in a particular quantum state.
- From the
statistical point of view there is a finite, but exceedingly small
possibility that a system that is well mixed could suddenly
``unmix'' and that all the air molecules in the room could suddenly
come to the front half of the room. The unlikelihood of this is well
described by Denbigh [Principles of Chemical Equilibrium,
1981] in a discussion of the behavior of an isolated system:
``In the case of systems containing an appreciable number of atoms,
it becomes increasingly improbable that we shall ever observe the
system in a non-uniform condition. For example, it is calculated
that the probability of a relative change of density,
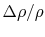 , of only
, of only 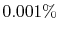 in
in
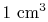 of air is smaller than
of air is smaller than
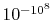 and would not be observed in trillions of years.
Thus, according to the statistical interpretation the discovery of
an appreciable and spontaneous decrease in the entropy of an
isolated system, if it is separated into two parts, is not
impossible, but exceedingly improbable. We repeat, however, that it
is an absolute impossibility to know when it will take
place.''
and would not be observed in trillions of years.
Thus, according to the statistical interpretation the discovery of
an appreciable and spontaneous decrease in the entropy of an
isolated system, if it is separated into two parts, is not
impossible, but exceedingly improbable. We repeat, however, that it
is an absolute impossibility to know when it will take
place.''
- The definition of entropy in the form
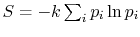 arises in other
aerospace fields, notably that of information theory. In this
context, the constant
arises in other
aerospace fields, notably that of information theory. In this
context, the constant 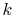 is taken as unity and the entropy becomes
a dimensionless measure of the uncertainty represented by a
particular message. There is no underlying physical connection with
thermodynamic entropy, but the underlying uncertainty concepts are
the same.
is taken as unity and the entropy becomes
a dimensionless measure of the uncertainty represented by a
particular message. There is no underlying physical connection with
thermodynamic entropy, but the underlying uncertainty concepts are
the same.
- The presentation of entropy in this subject is focused
on the connection to macroscopic variables and behavior. These
involve the definition of entropy given in
Chapter 5 of the notes and the physical link with
lost work, neither of which makes any mention of molecular
(microscopic) behavior. The approach in other sections of the notes
is only connected to these macroscopic processes and does not rely
at all upon the microscopic viewpoint. Exposure to the statistical
definition of entropy, however, is helpful as another way not only
to answer the question of ``What is entropy?'' but also to see the
depth of this fundamental concept and the connection with other
areas of technology.
UnifiedTP
|

