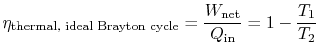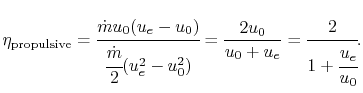11.2 Thermal and Propulsive Efficiency
It is
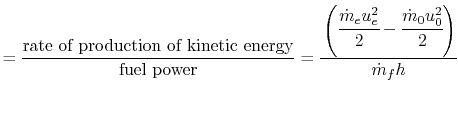
often convenient to break the overall efficiency into two parts:
thermal efficiency and propulsive efficiency, where
The thermal efficiency in this expression is the same as that which
we used extensively in Part I. For an ideal Brayton cycle it
is a function of the temperature ratio across the compressor,
Note that we can use our expression for thrust to rewrite the
equation for propulsive efficiency in a more convenient form,
then
UnifiedTP
|