11.3 Implications of propulsive efficiency for engine design
If we consider our expressions for thrust and propulsive efficiency
together,
we see that
Also note that for
where
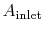 is the inlet area of an engine, shown in
Figure 11.1.
is the inlet area of an engine, shown in
Figure 11.1.
Figure 11.1:
Schematic of the inlet area of an engine
|
|
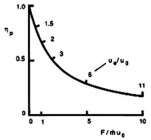
The balance between propulsive efficiency and specific thrust ( thrust per unit mass flow) is shown in
Figure 11.2.
thrust per unit mass flow) is shown in
Figure 11.2.
Figure 11.2:
Propulsive efficiency and
specific thrust as a function of exhaust velocity (Kerrebrock,
1991).
|
|
For fighter aircraft that need high thrust/weight and fly at high
speed, it is typical to employ engines with smaller inlet areas and
higher thrust per unit mass flow,
The small inlet of one of the F-22 Raptor's two engines is visible
just below the cockpit in Figure 11.3.
Figure 11.3:
The F-22 Raptor (Copyright 1999 by
Lockheed Martin).
|
|
However, transport aircraft that require higher efficiency and fly
at lower speeds usually employ engines with relatively larger inlet
areas and lower thrust per unit mass flow,
The large inlets of a Boeing 777-200's engines are shown in
Figure 11.4.
Figure 11.4:
The Boeing 777-200 (Jane's, 1998-9).
|
|
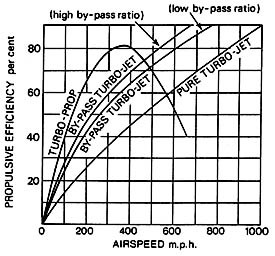
At low flight velocities, the highest propulsive efficiency is
typically obtained with a propeller or an unducted fan.
Figure 11.5 shows a propeller craft, and
Figure 11.6 shows a sketch of a jet engine with
an unducted fan. Figure 11.7 shows propulsive
efficiency as a function of airspeed for different engine bypass
ratios.
Figure 11.5:
A propeller gives a
relatively small impulse (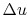 ) to a relatively large mass
flow (Boeing, 2000)
) to a relatively large mass
flow (Boeing, 2000)
|
|
Figure 11.6:
An advanced,
contour-rotating, unducted fan concept (Rolls-Royce, 1992)
|
|
Figure 11.7:
Propulsive efficiency
comparison for various gas turbine engine configurations
(Rolls-Royce, 1992)
|
|
UnifiedTP
|


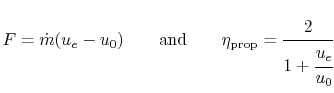
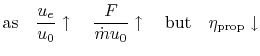
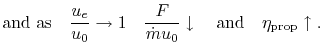
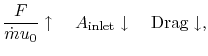
![]() thrust per unit mass flow) is shown in
Figure 11.2.
thrust per unit mass flow) is shown in
Figure 11.2.