- ... evidence1.1
- Alternatively, most thermodynamic
principles and can be derived from kinetic theory.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
applications1.2
-
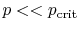 , and
, and
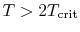 up to about
up to about
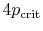 , [VW, S
& B: 3.4].
, [VW, S
& B: 3.4].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... behavior1.3
- See Section 5.2
for the other laws and credit for this form.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... substances2.1
- As an aside: The
derivative
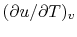 represents the slope of a
line of constant
represents the slope of a
line of constant 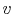 on a
on a 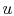 -
-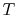 plane.
plane.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
terminology2.2
- Course Notes, ``Ideal Gases,'' Prof. Georg
Gyarmathy, Swiss Federal Institute of Technology, Zurich.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... hundred.2.3
- Adapted from Zemansky, M. W.,
and Dittman, R. H., ``Heat and Thermodynamics,'' Sixth Edition,
McGraw-Hill book company, 1981.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
substances.2.4
- Adapted from ``Engineering Thermodynamics,''
Reynolds, W. C., and Perkins, H. C., McGraw-Hill Publishers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... number2.5
- The Mach number,
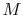 ,
is the ratio of the flow speed,
,
is the ratio of the flow speed, 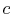 , to the speed of sound,
, to the speed of sound, 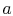 . You
will learn more about this quantity in fluids, but it is interesting
to see that
. You
will learn more about this quantity in fluids, but it is interesting
to see that 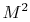 measures the ratio of the kinetic energy of the
gas to its thermal energy.
measures the ratio of the kinetic energy of the
gas to its thermal energy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
neglected)3.1
- In general this is a good assumption since in
typical combustion applications the fuel accounts for only about 5%
of the mass of the working fluid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... state3.2
- This fact is
often useful for solving thermodynamic cycles in different ways. For
instance, in this example we could sum the work terms all around the
cycle. Instead we will consider the difference between the heat
added to the cycle in process
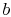 -
-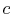 , and the heat rejected by the
cycle in process
, and the heat rejected by the
cycle in process 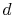 -
-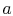 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
boundaries4.1
- Indeed, some ability to do work was lost, for we
could have put a piston in the volume and allowed the expansion of
the gas to do work to raise a weight.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... magnitude4.2
- Note that without our external work, the gas
would not move itself back into
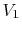 , even though such a
spontaneous reversal would be compatible with the First Law.
, even though such a
spontaneous reversal would be compatible with the First Law.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
explicit.5.1
- From notes of Professor F. E. C. Culick,
California Institute of Technology (with minor changes).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... irreversibility6.1
- This and the
following paragraph are excerpted with minor modifications from
A Course in Thermodynamics, Volume I, by J. Kestin,
Hemisphere Press (1979).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... surroundings)6.2
- In the
above equation, and in the arguments that follow, the quantities
 and
and
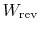 are both regarded as positive
for work done by the surroundings and heat given to the
surroundings. Although this is not in accord with the convention we
have been using, it seems to me, after writing the notes in both
ways, that doing this gives easier access to the ideas. I would be
interested in your comments on whether this perception is correct.
are both regarded as positive
for work done by the surroundings and heat given to the
surroundings. Although this is not in accord with the convention we
have been using, it seems to me, after writing the notes in both
ways, that doing this gives easier access to the ideas. I would be
interested in your comments on whether this perception is correct.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Perkins7.1
- Reynolds, W.C., and Perkins, H.C.,
Engineering Thermodynamics, McGraw-Hill Book Co., 1977.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... out8.1
- These
assumptions are reasonable for temperatures well below the critical
temperature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)11.1
- Here we
can switch from
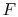 to the more mnemonic
to the more mnemonic 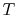 because temperature
will not play a significant role in our analysis.
because temperature
will not play a significant role in our analysis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... propulsive13.1
- The transmission efficiency
represents the ratio between compressor and turbine power, which is
less than unity due to parasitic frictional effects. As with the
combustion efficiency, however, this is very close to one and the
horizontal axis can thus be regarded essentially as propulsive
efficiency.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
negligible18.1
- Note: We don't need to make this assumption, and
if we were looking at the problem in detail we would solve it
numerically and not worry about whether an analytic solution
existed. In the present case, developing the analytic solution is
useful in presenting the structure of the solution as well as the
numbers, so we resort to the mild fiction of no heat transfer at the
fin end. We need to assess, after all is said and done, whether this
is appropriate or not.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
|

