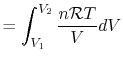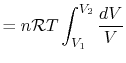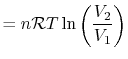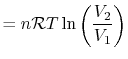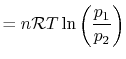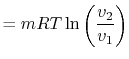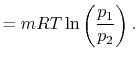Subsections
Changes in the state of a system are produced by interactions with
the environment through heat and work, which are two
different modes of energy transfer. During these interactions,
equilibrium (a static or quasi-static process) is necessary for the
equations that relate system properties to one-another to be valid.
1.3.1 Heat
Heat is energy
transferred due to temperature differences only.
- Heat transfer can alter system states;
- Bodies don't ``contain'' heat; heat is identified as it comes across system boundaries;
- The amount of heat needed to go from one state to another is path dependent;
- Adiabatic processes are ones in which no heat is transferred.
1.3.2 Zeroth Law of Thermodynamics
With the material we have discussed so far, we are now in a position
to describe the Zeroth Law. Like the other laws of thermodynamics
we will see, the Zeroth Law is based on observation. We start with
two such observations:
- If two bodies are in contact through a thermally-conducting
boundary for a sufficiently long time, no further observable changes
take place; thermal equilibrium is said to prevail.
- Two systems
which are individually in thermal equilibrium with a third are in
thermal equilibrium with each other; all three systems have the same
value of the property called temperature.
These closely connected ideas of temperature and thermal equilibrium
are expressed formally in the ``Zeroth Law of Thermodynamics:''
Zeroth Law: There exists for every thermodynamic system in
equilibrium a property called temperature. Equality of temperature
is a necessary and sufficient condition for thermal equilibrium.
The Zeroth Law thus defines a property (temperature) and
describes its behavior1.3.
Note that this law is true regardless of how we measure the property
temperature. (Other relationships we work with will typically
require an absolute scale, so in these notes we use either the
Kelvin
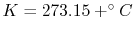 or Rankine
or Rankine
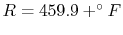 scales. Temperature scales will be discussed further in
Section 6.2.) The zeroth law is depicted
schematically in Figure 1.8.
scales. Temperature scales will be discussed further in
Section 6.2.) The zeroth law is depicted
schematically in Figure 1.8.
Figure 1.8:
The zeroth law schematically
|
|
[VW, S & B: 4.1-4.6]
Section 1.3.1 stated that heat is a way of changing
the energy of a system by virtue of a temperature difference only.
Any other means for changing the energy of a system is called
work. We can have push-pull work (e.g. in a piston-cylinder,
lifting a weight), electric and magnetic work (e.g. an electric
motor), chemical work, surface tension work, elastic work, etc. In
defining work, we focus on the effects that the system (e.g. an
engine) has on its surroundings. Thus we define work as being
positive when the system does work on the surroundings (energy
leaves the system). If work is done on the system (energy added to
the system), the work is negative.
Consider a simple compressible substance, for example, a gas (the
system), exerting a force on the surroundings via a piston, which
moves through some distance, 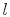 (Figure 1.9). The
work done on the surroundings,
(Figure 1.9). The
work done on the surroundings,
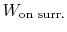 , is
, is
Why is the pressure 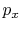 instead of
instead of 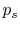 ? Consider
? Consider 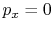 (vacuum). No work is done on the surroundings even
though
(vacuum). No work is done on the surroundings even
though 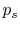 changes and the system volume changes.
changes and the system volume changes.
Use of 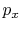 instead of
instead of 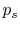 is often
inconvenient because it is usually the state of the system that we
are interested in. The external pressure can only be related to
the system pressure if
is often
inconvenient because it is usually the state of the system that we
are interested in. The external pressure can only be related to
the system pressure if
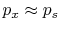 . For this to occur, there
cannot be any friction, and the process must also be slow enough so
that pressure differences due to accelerations are not significant.
In other words, we require a ``quasi-static'' process,
. For this to occur, there
cannot be any friction, and the process must also be slow enough so
that pressure differences due to accelerations are not significant.
In other words, we require a ``quasi-static'' process,
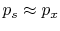 . Consider
. Consider
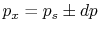 .
.
and the work done by the system is the same as the work done on the surroundings.
Under these conditions, we say that the process is ``reversible.''
The conditions for reversibility are that:
- If the process is reversed, the system and the surroundings will be returned to the
original states.
- To reverse the process we need to apply only an infinitesimal
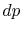 . A reversible process
can be altered in direction by infinitesimal changes in the external conditions (see Van
Ness, Chapter 2).
. A reversible process
can be altered in direction by infinitesimal changes in the external conditions (see Van
Ness, Chapter 2).
Remember this result, that we can only relate work done on
surroundings to system pressure for quasi-static (or reversible)
processes. In the case of a ``free expansion,'' where 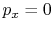 (vacuum),
(vacuum), 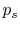 is not related to
is not related to 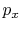 (and thus, not related to
the work) because the system is not in equilibrium.
(and thus, not related to
the work) because the system is not in equilibrium.
We can write the above expression for work done by the system in terms of the specific volume,
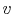 ,
,
where 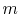 is the mass of the system. Note that if the system volume expands against a force, work is
done by the system. If the system volume contracts under a force, work is done on the
system.
is the mass of the system. Note that if the system volume expands against a force, work is
done by the system. If the system volume contracts under a force, work is done on the
system.
Figure 1.9:
A closed system (dashed box) against a piston, which moves into the surroundings
|
|
Figure 1.10:
Work during an irreversible process
|
|
For simple compressible substances in reversible processes,
the work done can be represented as the area under a curve in a
pressure-volume diagram, as in Figure 1.11(a).
Key points to note are the following:
- Properties only depend on states, but work is path dependent (depends on the path taken between states);
therefore work is not a property, and not a state variable.
- When we say
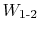 , the work between states 1 and 2, we need to specify the
path.
, the work between states 1 and 2, we need to specify the
path.
- For irreversible (non-reversible) processes, we cannot use
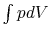 ;
either the work must be given or it must be found by another
method.
;
either the work must be given or it must be found by another
method.
Muddy Points
How do we know when work is done? (MP 1.3)
Consider Figure 1.12, which shows a system undergoing
quasi-static processes for which we can calculate work interactions
as 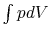 .
.
Figure 1.12:
Simple processes
|
|
Along Path a:
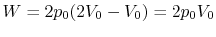
Along Path b:
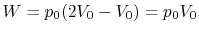
Practice Questions
Given a piston filled with air, ice, a bunsen burner, and a stack of
small weights, describe
- how you would use these to move along either path a or path b above,
and
- how you would physically know the work is different along each
path.
Consider the quasi-static, isothermal expansion of a thermally ideal
gas from 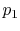 ,
, 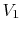 to
to 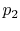 ,
, 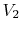 , as shown in
Figure 1.13. To find the work we must know the path.
Is it specified? Yes, the path is specified as isothermal.
, as shown in
Figure 1.13. To find the work we must know the path.
Is it specified? Yes, the path is specified as isothermal.
Figure 1.13:
Quasi-static, isothermal expansion of an ideal gas
|
|
The equation of state for a thermally ideal gas is
where 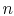 is the number of moles,
is the number of moles,
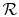 is the Universal gas
constant, and
is the Universal gas
constant, and 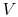 is the total system volume. We write the work as
above, substituting the ideal gas equation of state,
is the total system volume. We write the work as
above, substituting the ideal gas equation of state,
also for
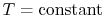 ,
,
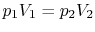 , so the work
done by the system is
, so the work
done by the system is
or in terms of the specific volume and the system mass,
We can have one, the other, or both: it depends on what crosses the
system boundary (and thus, on how we define our system). For example
consider a resistor that is heating a volume of water
(Figure 1.14):
Figure 1.14:
A resistor heating water
|
|
- If the water is the system, then the state of the
system will be changed by heat transferred from the resistor.
- If the
system is the water and the resistor combined, then the state
of the system will be changed by electrical work.
Douglas Quattrochi
2006-08-06
|


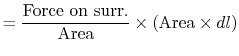
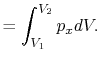
![]() instead of
instead of ![]() is often
inconvenient because it is usually the state of the system that we
are interested in. The external pressure can only be related to
the system pressure if
is often
inconvenient because it is usually the state of the system that we
are interested in. The external pressure can only be related to
the system pressure if
![]() . For this to occur, there
cannot be any friction, and the process must also be slow enough so
that pressure differences due to accelerations are not significant.
In other words, we require a ``quasi-static'' process,
. For this to occur, there
cannot be any friction, and the process must also be slow enough so
that pressure differences due to accelerations are not significant.
In other words, we require a ``quasi-static'' process,
![]() . Consider
. Consider
![]() .
.
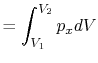
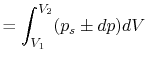
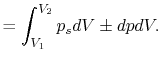
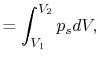
![]() (vacuum),
(vacuum), ![]() is not related to
is not related to ![]() (and thus, not related to
the work) because the system is not in equilibrium.
(and thus, not related to
the work) because the system is not in equilibrium.
![]() ,
,
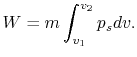
![]() .
.
![]()
![]()
![]() ,
, ![]() to
to ![]() ,
, ![]() , as shown in
Figure 1.13. To find the work we must know the path.
Is it specified? Yes, the path is specified as isothermal.
, as shown in
Figure 1.13. To find the work we must know the path.
Is it specified? Yes, the path is specified as isothermal.