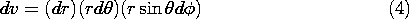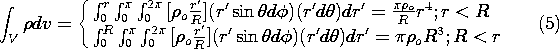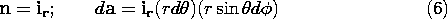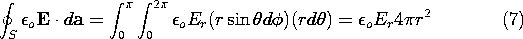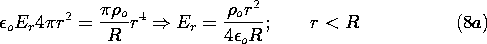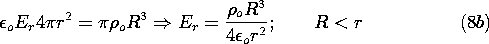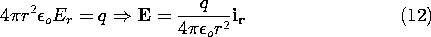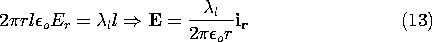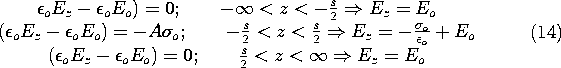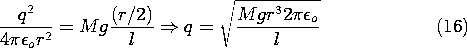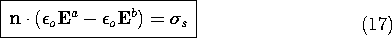1.3
Gauss' Integral Law of Electric Field Intensity
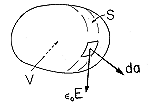
The Lorentz force law of Sec. 1.1 expresses the effect of electromagnetic fields on a moving charge. The remaining sections in this chapter are concerned with the reaction of the moving charges upon the electromagnetic fields. The first of Maxwell's equations to be considered, Gauss' law, describes how the electric field intensity is related to its source. The net charge within an arbitrary volume V that is enclosed by a surface S is related to the net electric flux through that surface by
With the surface normal defined as directed outward, the volume is shown in Fig. 1.3.1. Here the permittivity of free space,
o = 8.854 x 10-12 farad/meter, is an empirical constant needed to express Maxwell's equations in SI units. On the right in (1) is the net charge enclosed by the surface S. On the left is the summation over this same closed surface of the differential contributions of flux
da. The quantity
The following example illustrates the mechanics of carrying out the volume and surface integrations.
Figure 1.3.1 General surface S enclosing volume V.
Example 1.3.1. Electric Field Due to Spherically Symmetric Charge Distribution
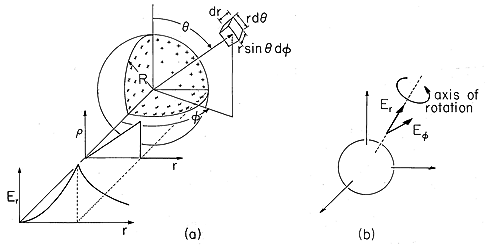
Given the charge and current distributions, the integral laws fully determine the electric and magnetic fields. However, they are not directly useful unless there is a great deal of symmetry. An example is the distribution of charge density
in the spherical coordinate system of Fig. 1.3.2. Here
o and R are given constants. An argument based on the spherical symmetry shows that the only possible component of E is radial.
Figure 1.3.2 (a) Spherically symmetric charge distribution, showing radial dependence of charge density and associated radial electric field intensity. (b) Axis of rotation for demonstration that the components of E transverse to the radial coordinate are zero.
Indeed, suppose that in addition to this r component the field possesses a
component. At a given point, the components of E then appear as shown in Fig. 1.3.2b. Rotation of the system about the axis shown results in a component of E in some new direction perpendicular to r. However, the rotation leaves the source of that field, the charge distribution, unaltered. It follows that E
also is zero.
The incremental volume element is
and it follows that for a spherical volume having arbitrary radius r,
To evaluate the left-hand side of (1), note that
Thus, for the spherical surface at the arbitrary radius r,
With the volume and surface integrals evaluated in (5) and (7), Gauss' law, (l), shows that
Inside the spherical charged region, the radial electric field increases with the square of the radius because even though the associated surface increases like the square of the radius, the enclosed charge increases even more rapidly. Figure 1.3.2 illustrates this dependence, as well as the exterior field decay. Outside, the surface area continues to increase in proportion to r2, but the enclosed charge remains constant.
Singular Charge Distributions
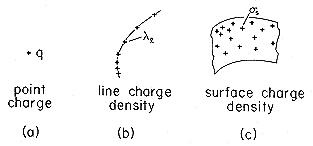
Examples of singular functions from circuit theory are impulse and step functions. Because there is only the one independent variable, namely time, circuit theory is concerned with only one "dimension." In three-dimensional field theory, there are three spatial analogues of the temporal impulse function. These are point, line, and surface distributions of
Figure 1.3.3 Singular charge distributions: (a) point charge, (b) line charge, (c) surface charge. A point charge is the limit of an infinite charge density occupying zero volume. With q defined as the net charge,
the point charge can be pictured as a small charge-filled region, the outside of which is charge free. An example is given in Fig. 1.3.2 in the limit where the volume 4
R3 /3 goes to zero, while q =
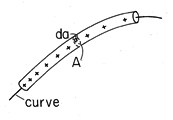
A line charge density represents a two-dimensional singularity in charge density. It is the mathematical abstraction representing a thin charge filament. In terms of the filamentary volume shown in Fig. 1.3.4, the line charge per unit length
l (the line charge density) is defined as the limit where the cross-sectional area of the volume goes to zero,
Figure 1.3.4 Filamentary volume element having cross-section da used to define line charge density.
remains finite. In general,
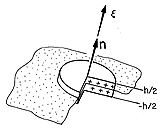
The one-dimensional singularity in charge density is represented by the surface charge density. The charge density is very large in the vicinity of a surface. Thus, as a function of a coordinate perpendicular to that surface, the charge density is a one-dimensional impulse function. To define the surface charge density, mount a pillbox as shown in Fig. 1.3.5 so that its top and bottom surfaces are on the two sides of the surface. The surface charge density is then defined as the limit
Figure 1.3.5 Volume element having thickness h used to define surface charge density. Figure 1. Point charge q at origin of spherical coordinate system.
where the
coordinate is picked parallel to the direction of the normal to the surface, n. In general, the surface charge density
s is a function of position in the surface.
Illustration. Field of a Point Charge
A point charge q is located at the origin in Fig. 1.3.6. There are no other charges. By the same arguments as used in Example 1.3.1, the spherical symmetry of the charge distribution requires that the electric field be radial and be independent of
is the electric field associated with a point charge q.
Illustration. The Field Associated with Straight Uniform Line Charge
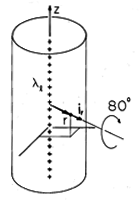
A uniform line charge is distributed along the z axis from z = -
to z = +\infty, as shown in Fig. 1.3.7. For an observer at the radius r, translation of the line source in the z direction and rotation of the source about the z axis (in the
Figure 1.3.7 Uniform line charge distributed from - infinity to + infinity along z axis. Rotation by 180 degrees about axis shown leads to conclusion that electric field is radial. This time, Gauss' integral law is applied using for S the surface of a right circular cylinder coaxial with the z axis and of arbitrary radius r. Contributions from the ends are zero because there the surface normal is perpendicular to E. With the cylinder taken as having length l, the surface integration amounts to a multiplication of
for the field of an infinitely long uniform line charge having density
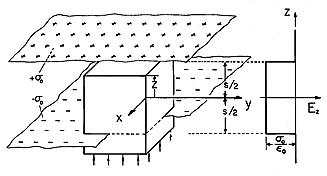
Example 1.3.2. The Field of a Pair of Equal and Opposite Infinite Planar Charge Densities
Consider the field produced by a surface charge density +
First, the field must be z directed. Indeed there cannot be a component of E transverse to the z axis, because rotation of the system around the z axis leaves the same source distribution while rotating that component of E. Hence, no such component exists.
Figure 1.3.8 Sheets of surface charge and volume of integration with upper surface at arbitrary position x. With field Eo due to external charges equal to zero, the distribution of electric field is the discontinuous function shown at right. Because the source distribution is independent of x and y, Ez is independent of these coordinates. The z dependence is now established by means of Gauss' integral law, (1). The volume of integration, shown in Fig. 1.3.8, has cross-sectional area A in the x-y plane. Its lower surface is located at an arbitrary fixed location below the lower surface charge distribution, while its upper surface is in the plane denoted by z. For now, we take Ez as being Eo on the lower surface. There is no contribution to the surface integral from the side walls because these have normals perpendicular to E. It follows that Gauss' law, (1), becomes
That is, with the upper surface below the lower charge sheet, no charge is enclosed by the surface of integration, and Ez is the constant Eo. With the upper surface of integration between the charge sheets, Ez is Eo minus
Illustration. Coulomb's Force Law for Point Charges
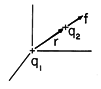
It is worthwhile to see that for charges at rest, Gauss' integral law and the Lorentz force law give the familiar action at a distance force law. The force on a charge q is given by the Lorentz law, (1.1.1), and if the electric field is caused by a second charge at the origin in Fig. 1.3.9, then
Figure 1.3.9. Coulomb force induced on charge q2 due to field from q1.
Coulomb's famous statement that the force exerted by one charge on another is proportional to the product of their charges, acts along a line passing through each charge, and is inversely proportional to the square of the distance between them, is now demonstrated.
Demonstration 1.3.1. Coulomb's Force Law
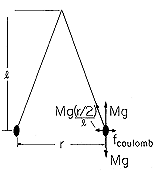
The charge resulting on the surface of adhesive tape as it is pulled from a dispenser is a common nuisance. As the tape is brought toward a piece of paper, the force of attraction that makes the paper jump is an aggravating reminder that there are charges on the tape. Just how much charge there is on the tape can be approximately determined by means of the simple experiment shown in Fig. 1.3.10.
Figure 1.3.10. Like-charged particles on ends of thread are pushed apart by the Coulomb force. Two pieces of freshly pulled tape about 7 cm long are folded up into balls and stuck on the ends of a thread having a total length of about 20 cm. The middle of the thread is then tied up so that the charged balls of tape are suspended free to swing. (By electrostatic standards, our fingers are conductors, so the tape should be manipulated chopstick fashion by means of plastic rods or the like.) It is then easy to measure approximately l and r, as defined in the figure. The force of repulsion that separates the "balls" of tape is presumably predicted by (15). In Fig. 1.3.10, the vertical component of the tension in the thread must balance the gravitational force Mg (where g is the gravitational acceleration and M is the mass). It follows that the horizontal component of the thread tension balances the Coulomb force of repulsion.
As an example, tape balls having an area of A = 14 cm2, (7 cm length of 2 cm wide tape) weighing 0.1 mg and dangling at a length l = 20 cm result in a distance of separation r = 3 cm. It follows from (16) (with all quantities expressed in SI units) that q = 2.7 x 10-9 coulomb. Thus, the average surface charge density is q/A = 1.9 x 10-6 coulomb/meter or 1.2 x 1013 electronic charges per square meter. If these charges were in a square array with spacing s between charges, then
m. This length is at the limit of an optical microscope and may seem small. However, it is about 1000 times larger than a typical atomic dimension.
2 An alternative way to charge a particle, perhaps of low density plastic, is to place it in the corona discharge around the tip of a pin placed at high voltage. The charging mechanism at work in this case is discussed in Chapter 7 (Example 7.7.2).
