The heat generated by electromagnetic fields is often the controlling
feature of an engineering design. Semiconductors inevitably produce
heat, and the distribution and magnitude of the heat source is an
important consideration whether the application is to computers or
power conversion. Often, the generation of heat poses a fundamental
limitation on the performance of equipment. Examples where
the generation of heat is desirable include the heating coil of an
electric stove and the microwave irradiation of food in a microwave
oven.
Ohmic conduction is the primary cause of heat generation in metals,
but it also operates in semiconductors, electrolytes, and (at low
frequencies) in semi-insulating liquids and solids. The
mechanism responsible for this type of heating was discussed in Sec.
11.3. The dissipation density associated with Ohmic conduction is
 E
E  E.
E.
An Ohmic current can be imposed by making electrical contact with
the material, as for the heating element in a stove. If the
material is a good conductor, such currents can also be induced by
magnetic induction (without electrical contact). The currents
induced by time-varying magnetic fields in Chap. 10 are an example.
Induction
heating is an MQS process and often used in processing metals.
Currents induced in transformer cores by
the time-varying magnetic flux are an example of undesirable
heating. In this context, the associated losses (which are
minimized by laminating the core) are said to be due to eddy
currents.
Ohmic heating can also be induced by "capacitive" coupling. In
the EQS examples of Sec. 7.9, dielectric heating is caused by the
currents associated with the accumulation of unpaired charges.
Whether due to magnetic induction or capacitive coupling, the
generation of heat is described by the dissipation density Pd =
 E
E  E identified in Sec. 11.3. However, the
polarization and magnetization terms in the conservation theorem,
(11.2.7), can also be responsible for energy dissipation. This occurs
when the (electric or magnetic) dipoles do not align instantaneously
with the fields. The polarization and magnetization constitutive
laws differ from the laws postulated in Sec. 11.3.
E identified in Sec. 11.3. However, the
polarization and magnetization terms in the conservation theorem,
(11.2.7), can also be responsible for energy dissipation. This occurs
when the (electric or magnetic) dipoles do not align instantaneously
with the fields. The polarization and magnetization constitutive
laws differ from the laws postulated in Sec. 11.3.
As an example suggesting how the polarization term in (11.2.7)
can represent dissipation, picture the artificial dielectric of
Demonstration 6.6.1 (the ping-pong ball dielectric) but with spheres
that are highly resistive rather than perfectly conducting. The
accumulation of charge on the poles of the spheres in response to the
application of an electric field is described by a rate,
rather than a magnitude, that is proportional to the field. Thus,
we would expect 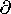 P/
P/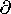 t rather than P to be proportional
to E. With
t rather than P to be proportional
to E. With  a coefficient representing the properties and
geometry of the spheres, the polarization constitutive law would then
take the form
a coefficient representing the properties and
geometry of the spheres, the polarization constitutive law would then
take the form

If this law is used to express the polarization term in the
conservation law, the second term on the right in (11.2.7), a
positive definite quantity results.

As might be expected from the physical origins of the constitutive
law, the polarization term now represents dissipation rather than
energy storage.
When materials are placed in electric fields having frequencies so
high that conduction effects are negligible, losses due to
the polarization of dipoles become the dominant heating mechanism.
The artificial diamagnetic material considered in Demonstration 9.5.1
suggests how analogous losses are associated with the dynamic
magnetization of a material. If the spherical particles comprising
the artificial diamagnetic material have a finite conductivity, the
induced dipole moments are not in phase with an applied sinusoidal
field. What amounts to Ohmic dissipation on the particle scale is
accounted for on the macroscopic scale by a modified constitutive law
of magnetization.
The most common losses due to magnetization are encountered in
ferromagnetic materials. Hysteresis losses occur because of the
coercion required to obtain alignment of ferromagnetic domains. We
will end this section with the relationship between the hysteresis
curve of Fig. 9.4.6 and the dissipation density.
Energy Conservation for Temporally Periodic Systems
Many practical situations involve fields that vary with time in a
periodic fashion. The sinusoidal steady state is the most common
example. If the energy conservation law (11.0.8) is integrated
over one period T, the energy storage term makes no contribution.
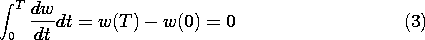
As a result, the time average of the conservation law states that
the time average of the input power goes into the time average of the
dissipation. The time average of the integral form of the
conservation law, (11.1.1), becomes
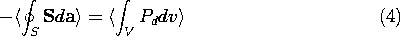
This expression, which assumes that the dynamics are periodic but not
necessarily sinusoidal, gives us two ways to compute the total energy
dissipation. Either we can use the right-hand side and integrate the
power dissipation density over the volume, or we can use the
left-hand side and integrate the time average of S  da
over the surface enclosing the volume.
da
over the surface enclosing the volume.
Consider the sinusoidal steady state as a particular case. If
P and M are related to E and H by linear differential
equations, an approach can be taken that is familiar from circuit
theory. The phase and amplitude of each field at a given location are
represented by a complex amplitude. For example, the electric and
magnetic field intensities are written as
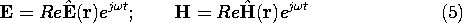
A complex vector 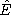 (r) has three complex scalar
components
(r) has three complex scalar
components 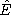 x (r),
x (r), 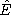 y (r), and
y (r), and
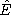 z(r). The meaning of each is the same as the meaning
of a
complex voltage in circuit theory: e.g., the magnitude of
z(r). The meaning of each is the same as the meaning
of a
complex voltage in circuit theory: e.g., the magnitude of 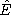 x(r), |
x(r), |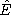 x(r)|, gives the peak amplitude of the
x component of the electric field varying cosinusoidally with time,
and the phase of
x(r)|, gives the peak amplitude of the
x component of the electric field varying cosinusoidally with time,
and the phase of 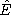 x(r) gives the phase advance of the
cosine time function.
x(r) gives the phase advance of the
cosine time function.
In determining the time averages of products of quantities that
are in the sinusoidal steady state, it is helpful to make use of the
time average theorem. With * designating the complex conjugate,

This can be shown by using the identity
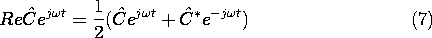
Induction Heating
In this case, the heating is represented by
Ohmic conduction and Pd given by (11.3.3c). The examples from
Chaps. 7 and 10 involving conductors of finite conductivity offer the
opportunity to apply this relation to the evaluation of the right-hand
side of (4). If the same total time average power is calculated
using the left-hand side of this expression, it may seem that Ohm's
law is not required. However, remember that this law is also
reflected in the field quantities used to calculate S.
Example 11.5.1. Induction Heating of the Thin Shell
The thin conducting shell of Fig. 11.5.1, in a field Ho(t)
applied collinear with its axis, was described in Example 10.3.1.
Here the applied field is in the sinusoidal steady state

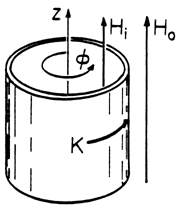 Figure 11.5.1 Circular
cylindrical conducting shell in imposed axial magnetic field
intensity Ho(t)
Figure 11.5.1 Circular
cylindrical conducting shell in imposed axial magnetic field
intensity Ho(t)
According to (10.3.9), the complex amplitude of the response,
the magnetic field inside the shell, is

where  m =
m = 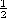
 o
o 
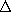 a.
a.
The complex amplitude of the surface current density circulating
in the shell follows from (10.3.8).
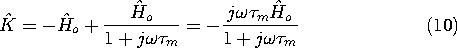
Because the current density is uniform over the radial
cross-section of the shell, the dissipation density can be written
in terms of the surface current density K = 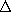
 E.
E.

It follows from the application of the time average theorem, (6),
that the total time average dissipation is
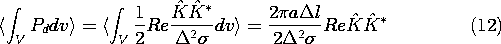
where l is the shell length.
To complete the derivation based on an integration of the density over
the volume of the conductor, this expression can be evaluated using
(10).
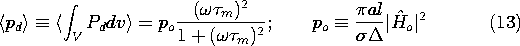
The same result is found by evaluating the time average of the
Poynting flux density integrated over a surface that is just outside
the shell at r = a. To see this, we again use the time average
theorem, (6), and recognize that the surface integral amounts to a
multiplication by the surface area of the shell.
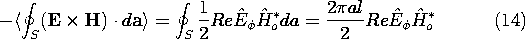
To evaluate this expression, (10) is used to determine
E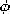
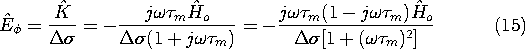
Evaluation of (14) then gives
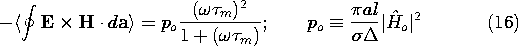
which is the same result as found by integrating the dissipation
density over the volume, (13).
The dependence of the time average power dissipation on the
normalized frequency is shown in Fig. 11.5.2. At very low
frequencies, the induced current is not large enough to have an
appreciable effect on the imposed field. Thus, the electric field is
proportional to the time rate of change of the applied field,
and because the dissipation is proportional to the square of E,
the power dissipation increases as the square of 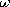 . At high
frequencies, the induced current can be no more than that required to
shield the imposed field from the region inside the shell. As a
result, the dissipation reaches an asymptotic limit.
. At high
frequencies, the induced current can be no more than that required to
shield the imposed field from the region inside the shell. As a
result, the dissipation reaches an asymptotic limit.
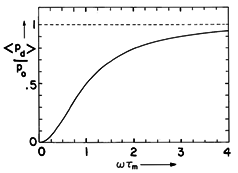 Figure 11.5.2 Time average power dissipation density
normalized to po as defined with (13) as a function of the
frequency normalized to the magnetic diffusion time defined with
(9).
Figure 11.5.2 Time average power dissipation density
normalized to po as defined with (13) as a function of the
frequency normalized to the magnetic diffusion time defined with
(9).
Which of the two approaches is best for finding the total power
dissipation? The answer depends on what field information is
available. Certainly, the notion that the total heat generated can be
found by integrating over a surface that is completely outside the
heated material is a fundamental consequence of Poynting's theorem.
Dielectric Heating
In the sinusoidal steady state, we can
identify the power dissipation density associated with polarization by
finding the time average

In view of the time average theorem, (6), this becomes

If the polarization P does not follow the electric field E
instantaneously, yet the material is still linear and isotropic, the
complex vector 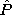 can be related to
can be related to 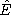 by a
complex susceptibility. Or, instead, the complex displacement flux
density vector
by a
complex susceptibility. Or, instead, the complex displacement flux
density vector 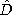 is related to
is related to 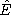 by a complex
dielectric constant.
by a complex
dielectric constant.

Here  is the complex permittivity with real and
imaginary parts
is the complex permittivity with real and
imaginary parts  ' and -
' and - ", respectively.
", respectively.
Evaluation of (18) using this constitutive law gives
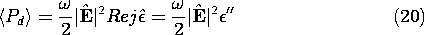
Thus,  " represents the electrical dissipation associated with the
polarization process.
" represents the electrical dissipation associated with the
polarization process.
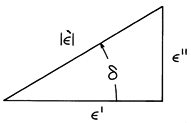 Figure 11.5.3 Definition of angle
Figure 11.5.3 Definition of angle
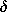 defining the loss tangent tan(
defining the loss tangent tan( 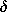 ) in terms of the
real and the negative of the imaginary parts of the complex
permittivity.
) in terms of the
real and the negative of the imaginary parts of the complex
permittivity.
In the literature, the loss tangent tan 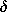 is often used
to represent dissipation. It is the tangent of the phase angle
is often used
to represent dissipation. It is the tangent of the phase angle
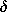 of the complex dielectric constant defined in terms
of the complex dielectric constant defined in terms  '
and
'
and  " in Fig. 11.5.3. Thus,
" in Fig. 11.5.3. Thus,
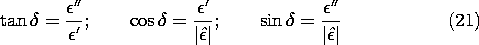
From this definition, it follows from Eulers formula that
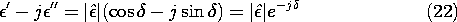
Given the complex amplitude of the electric field, D
is

If the electric field is Eo cos ( t), then D is
|
t), then D is
|  | Eo cos (
| Eo cos ( t -
t - 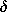 ). The electric
displacement lags the electric field by the phase angle
). The electric
displacement lags the electric field by the phase angle 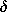 .
.
In terms of the loss tangent defined by (21), the time average
electrical dissipation density of (20) becomes

Usually the loss tangent and  ' are measured. In the
following example, we compute the complex permittivity from a model of
the polarizable medium and find the electrical dissipation on a
macroscopic basis. In this special case we have the option of
finding the time average loss by considering each of the dipoles
on a microscopic basis. This is not generally possible, because the
interactions among dipoles that are neglected in this example are
usually too complicated for an analytic treatment.
' are measured. In the
following example, we compute the complex permittivity from a model of
the polarizable medium and find the electrical dissipation on a
macroscopic basis. In this special case we have the option of
finding the time average loss by considering each of the dipoles
on a microscopic basis. This is not generally possible, because the
interactions among dipoles that are neglected in this example are
usually too complicated for an analytic treatment.
Example 11.5.2. An Artificial Lossy Dielectric
By putting together examples considered in Chaps. 6 and 7, we can
illustrate the origins of the complex permittivity. The artificial
dielectric of Example 6.6.1 and Demonstration 6.6.1 had "molecules"
consisting of perfectly conducting spheres. As a result, the
polarization was pictured as instantaneously in step with the applied
field. We consider now the result of having spheres that have finite
conductivity.
The response of a single sphere having a finite conductivity
 and permittivity
and permittivity  surrounded by free space is a special
case of Example 7.9.3. The response to a sinusoidal drive
is summarized by (7.9.36), where we set
surrounded by free space is a special
case of Example 7.9.3. The response to a sinusoidal drive
is summarized by (7.9.36), where we set  a = 0,
a = 0,  a =
a =  o,
o,
 b =
b =  , and
, and  b =
b =  . All
that is required from this solution for the potential is the moment of
a dipole that would give rise to the same exterior field as does the
sphere. Comparison of the potential of a dipole, (4.4.10), to that
given by (7.9.36a) shows that the complex amplitude of the moment
is
. All
that is required from this solution for the potential is the moment of
a dipole that would give rise to the same exterior field as does the
sphere. Comparison of the potential of a dipole, (4.4.10), to that
given by (7.9.36a) shows that the complex amplitude of the moment
is
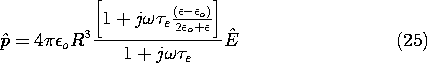
where  e
e  (2
(2 o +
o +  )/
)/ . If mutual
interactions between dipoles are ignored, the polarization density
P is this moment of a single dipole multiplied by the number of
dipoles per unit volume, N. For a cubic array with a distance s
between the dipoles (the centers of the spheres), N = 1/s3. Thus,
the complex amplitude of the electric displacement is
. If mutual
interactions between dipoles are ignored, the polarization density
P is this moment of a single dipole multiplied by the number of
dipoles per unit volume, N. For a cubic array with a distance s
between the dipoles (the centers of the spheres), N = 1/s3. Thus,
the complex amplitude of the electric displacement is
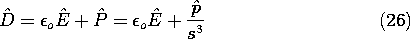
Combining this result with the moment given by (25) yields the desired
constitutive law in the form 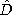 =
= 
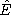 ,
where the complex permittivity is
,
where the complex permittivity is
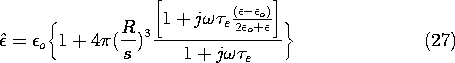
The time average power dissipation density follows from this
expression and (20).
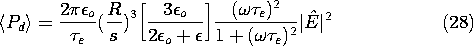
The dependence of the power dissipation on frequency has the same
form as for the induction heating example, Fig. 11.5.2. At low
frequencies, the surface charges induced at the north and south poles
of each sphere are completely determined by the external field. Thus,
the current density within the sphere that makes possible the
accumulation of these surface charges is proportional to the time rate
of change of the applied field. At low frequencies, the dissipation
is proportional to the square of the volume current and hence to the
square of the time rate of change of the applied field. As a result,
at low frequencies, the dissipation density increases with the square
of the frequency.
As the frequency is raised, less surface charge is induced on the
spheres. Although the
amount of charge induced is inversely proportional to the frequency,
there is a compensating effect because the volume currents are
responsible for the dissipation, and these are proportional to the
time rate of change of the charge. Thus, the dissipation density
reaches a saturation value as the frequency becomes very high.
One tool used to form a picture of atomic, molecular, and domain
physics is dielectric spectroscopy. Using this approach, the
frequency dependence of the complex permittivity is used to gain
insight into the microscopic structure.
Magnetization, like polarization, can also be the source of
dissipation. The time average dissipation density due to
magnetization follows by taking the time averge of the third and
fourth terms on the right in the basic power theorem, (11.2.7).
Combined, these terms give

For small-signal applications, this source of dissipation is dealt
with by introducing a complex permeability 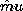 such that
such that 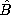 =
= 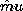
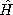 . The role of the complex
permeability is similar to that of the complex permittivity.
The artificial diamagnetic material of Example 9.5.2 and
Demonstration 9.5.1 can be used to exemplify the concept. Instead of
perfectly conducting spheres that give rise to a magnetic
moment instantaneously induced antiparallel to the applied field,
spherical shells of finite conductivity would be used. The dipole
moment induced in the individual spherical shells would be deduced
following the same approach as in Sec. 10.4. The resulting dipole
moment would not be in phase with an applied sinusoidally varying
magnetic field. The derivation of an equivalent complex permeability
would follow from the same line of reasoning as used in the previous
example.
. The role of the complex
permeability is similar to that of the complex permittivity.
The artificial diamagnetic material of Example 9.5.2 and
Demonstration 9.5.1 can be used to exemplify the concept. Instead of
perfectly conducting spheres that give rise to a magnetic
moment instantaneously induced antiparallel to the applied field,
spherical shells of finite conductivity would be used. The dipole
moment induced in the individual spherical shells would be deduced
following the same approach as in Sec. 10.4. The resulting dipole
moment would not be in phase with an applied sinusoidally varying
magnetic field. The derivation of an equivalent complex permeability
would follow from the same line of reasoning as used in the previous
example.
Hysteresis Losses
Under periodic conditions in magnetizable solids, B and H are
related by the hysteresis curve described in Sec. 9.4 and illustrated
again in Fig. 11.5.4. What time average power dissipation is implied
by the hysteresis?
As before, B and H are collinear. However, neither is now a
single-valued function of the other. Evaluation of (29) is
accomplished by breaking the cycle into two parts, each involving a
single-valued relationship between B and H. The first is the
upswing "trajectory" from A 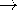 C in Fig. 11.5.4. Over
this half-cycle, which takes B from BA to BC, the trajectory
is H+(B). With B taken as BA when t = 0, it follows from
(11.4.4) and (11.4.5) that
C in Fig. 11.5.4. Over
this half-cycle, which takes B from BA to BC, the trajectory
is H+(B). With B taken as BA when t = 0, it follows from
(11.4.4) and (11.4.5) that
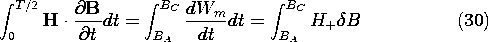
This is the area under the curve of H versus B between A and
C in Fig. 11.5.4, traversed on the "upswing." A similar
evaluation for the "downswing," where the trajectory is H-(B),
gives
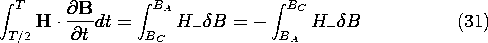
The time average power dissipation, (29), then is the sum of these
two contributions divided by T.
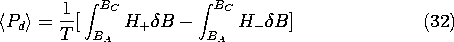
Thus, the area within the hysteresis loop is the energy dissipated in
one cycle.
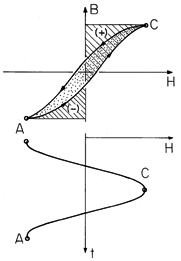 Figure 11.5.4 With the
application of a sinusoidal magnetic field intensity, a steady state
is reached in which the hysteresis loop shown in the B-H plane is
traced out in the direction shown. The dashed area represents the
energy density associated with upward traversal from A to C. The
dotted area inside the loop represents the energy density dissipated
per traversal of the loop.
Figure 11.5.4 With the
application of a sinusoidal magnetic field intensity, a steady state
is reached in which the hysteresis loop shown in the B-H plane is
traced out in the direction shown. The dashed area represents the
energy density associated with upward traversal from A to C. The
dotted area inside the loop represents the energy density dissipated
per traversal of the loop.

