

|
|
| Thermodynamics and Propulsion | |
Subsections
11.6 Performance of Jet EnginesIn Chapter 3 we represented a gas turbine engine using a Brayton cycle and derived expressions for efficiency and work as functions of the temperature at various points in the cycle. In this section we will perform further ideal cycle analysis to express the thrust and fuel efficiency of engines in terms of useful design variables, including design limits, flight conditions, and design choices. The expressions we develop will allow us to define a particular mission and then determine the optimum component characteristics (e.g. compressor, combustor, turbine) for an engine for a given mission. Note that ideal cycle analysis addresses only the thermodynamics of the airflow within the engine. It does not describe the details of the components (the blading, the rotational speed, etc.), but only the results the various components produce (e.g. pressure ratios, temperature ratios). In Chapter 12 we will look in greater detail at how some of the components (the turbine and the compressor) produce these effects.
11.6.1 Notation and station numberingNotation:
where the capital subscript
11.6.2 Ideal Assumptions
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
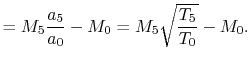 |
![$\displaystyle \frac{P_t}{P} = \left[1+\frac{\gamma-1}{2}M^2\right]^{\frac{\gamma}{\gamma-1}},$](img1296.png)
The ratios of stagnation pressure to static pressure at inlet and exit of the ramjet are
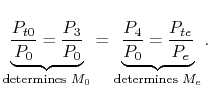
The ratios of stagnation to static pressure at exit and at inlet are the same, with the consequence that the inlet and exit Mach numbers are also the same.
To find the thrust we need to find the ratio of the temperature at exit and the temperature at inlet. This is given by
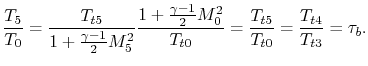
where
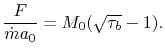
From the steady flow energy equation:
The exit mass flow is not greatly different from the inlet mass flow,
with
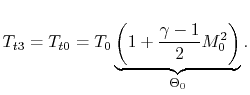
Thus, the fuel-air ratio is
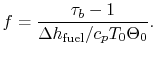
The fuel-air ratio,
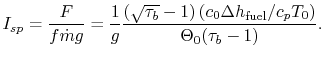
The specific impulse can be written in terms of fuel properties and flight and vehicle characteristics as
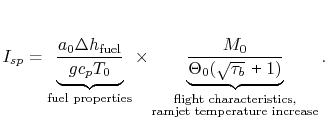
We wish to explore the parameter dependency of the above expression, which is a complicated formula. How can we do this? What are the important effects of the different parameters? How do we best capture the ramjet performance behavior?
To make effective comparisons, we need to add some additional
information concerning the operational behavior. An important case
to examine is when we have stoichiometric conditions and all the
fuel burns (denoted by
![]() ). What happens in this
situation as the flight Mach number,
). What happens in this
situation as the flight Mach number, ![]() , increases?
, increases? ![]() is
fixed so
is
fixed so ![]() increases, but the maximum temperature does not
increase much because of dissociation: the reaction does not go to
completion at high temperature. A useful approximation is therefore
to take
increases, but the maximum temperature does not
increase much because of dissociation: the reaction does not go to
completion at high temperature. A useful approximation is therefore
to take ![]() constant for stoichiometric operation. In the
stratosphere, from 10 to 30 km,
constant for stoichiometric operation. In the
stratosphere, from 10 to 30 km,
![]() . The maximum temperature ratio is
. The maximum temperature ratio is
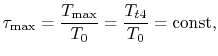
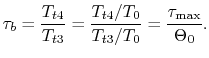
For the stoichiometric ramjet,
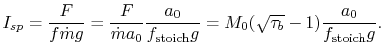
Using the expression for
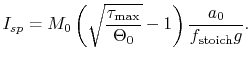
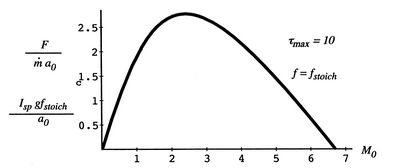
|
A plot of the performance of the stoichiometric ramjet is shown in
Figure 11.14. The figure shows that for the
parameters used, the best operating range of a hydrocarbon-fueled
ramjet is
![]() . The parameters used are
. The parameters used are
![]() ,
,
![]() in the stratosphere,
in the stratosphere,
![]() for hydrocarbons, such that
for hydrocarbons, such that
![]() .
.
Between Section 3.7.3 and this section we have:
Muddy Points
What exactly is the specific impulse, ![]() , a measure of?
(MP 11.1)
, a measure of?
(MP 11.1)
How is ![]() found for rockets in space where
found for rockets in space where
![]() ?
(MP 11.2)
?
(MP 11.2)
Why does industry use ![]() rather than
rather than ![]() ? Is there an
advantage to this? (MP 11.3)
? Is there an
advantage to this? (MP 11.3)
Why isn't mechanical efficiency an issue with ramjets? (MP 11.4)
How is thrust created in a ramjet? (MP 11.5)
What is the relation between
![]() and the
existence of the maximum value of
and the
existence of the maximum value of ![]() ?
(MP 11.6)
?
(MP 11.6)
Why didn't we have a 2s point for the Brayton cycle with non-ideal components? (MP 11.7)
What is the variable
![]() ? (MP 11.8)
? (MP 11.8)
We now examine an engine with turbomachinery, as shown in Figure 11.15. Methodology:
![$\displaystyle F = \dot{m}(u_7-u_0) \quad \Rightarrow \quad \frac{F}{\dot{m}a_0} = M_0\left[\frac{u_7}{u_0}-1\right] \quad \textrm{(can neglect fuel)},$](img1335.png) |
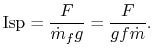 |
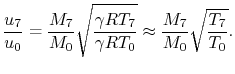 |
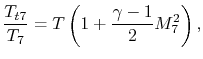 |
 |
||
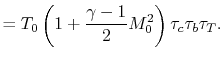 |
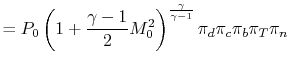 |
||
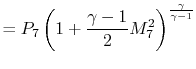 |
||
|
and
| ||
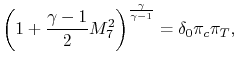 |
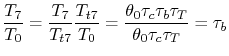 |
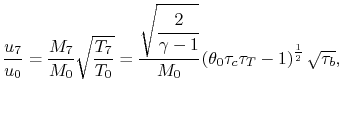 |
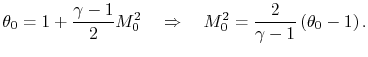 |
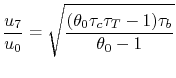 |
The steady flow energy equation states
Since the turbine shaft is connected to the compressor shaft
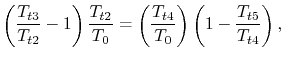 |
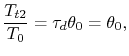 |
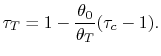 |
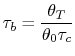 |
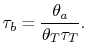 |
![$\displaystyle \frac{F}{\dot{m}a_0} = M_0\left[\left\{\left(\frac{\theta_0}{\the...
..._c} \right\}^\frac{1}{2}-1\right] \quad \textrm{Specific thrust for a turbojet}$](img1371.png) |
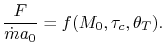 |
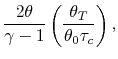 |
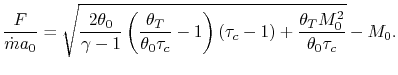 |
 |
||
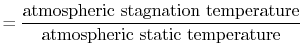 |
||
Our final step involves writing the specific impulse and other measures of efficiency in terms of these same parameters. We begin by writing the First Law across the combustor to relate the fuel flow rate and heating value of the fuel to the total enthalpy rise.
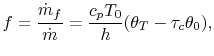 |
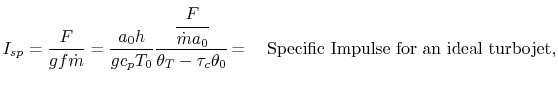 |
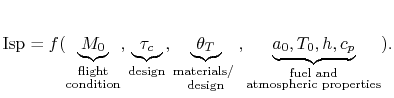 |
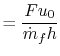 |
||
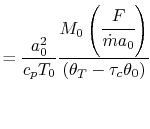 |
||
|
or
| ||
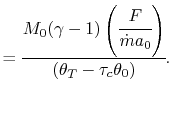 |
||
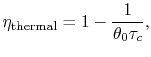 |
| Mach number | Altitude | Ambient Temp. | Speed of sound |
| 0 | Sea level | 288 K | 340 m/s |
| 0.85 | 12 km | 217 K | 295 m/s |
| 2.0 | 18 km | 217 K | 295 m/s |
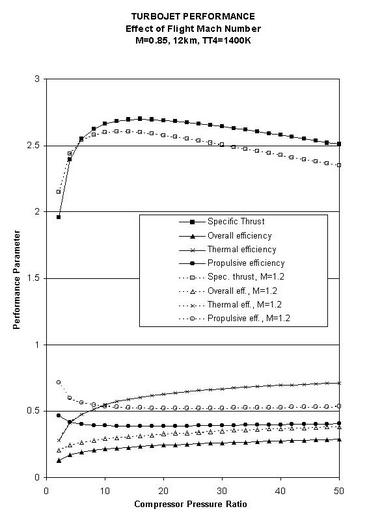
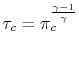 |
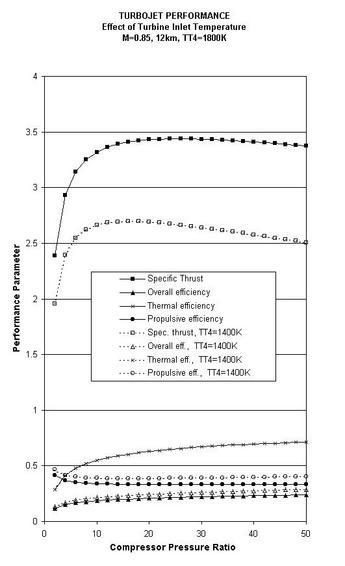
|
|
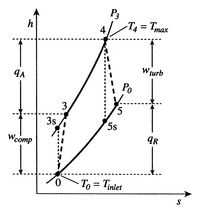
To conclude this chapter, we will now improve our estimates of cycle performance by including the effects of irreversibility. We will use the Brayton cycle as an example. What are the sources of non-ideal performance and departures from reversibility?
We take into account here only irreversibility in the compressor and
in the turbine. Because of these irreversibilities, we need more
work,
![]() (the changes in kinetic energy from
inlet to exit of the compressor are neglected), to drive the
compressor than in the ideal situation. We also get less work,
(the changes in kinetic energy from
inlet to exit of the compressor are neglected), to drive the
compressor than in the ideal situation. We also get less work,
![]() , back from the turbine. The consequence, as
can be inferred from Figure 11.19, is that the
net work from the engine is less than in the cycle with ideal
components.
, back from the turbine. The consequence, as
can be inferred from Figure 11.19, is that the
net work from the engine is less than in the cycle with ideal
components.
|
To develop a quantitative description of the effect of these departures from reversible behavior, consider a perfect gas with constant specific heats and neglect kinetic energy at the inlet and exit of the turbine and compressor. We define the turbine adiabatic efficiency as
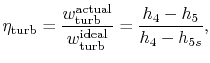 |
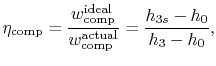
again for the same pressure ratio. Note that for the turbine the ratio is the actual work delivered divided by the ideal work, whereas for the compressor the ratio is the ideal work needed divided by the actual work required. These are not thermal efficiencies, but rather measures of the degree to which the compression and expansion approach the ideal processes.
We now wish to find the net work done in the cycle and the efficiency. The net work is given either by the difference between the heat received and rejected or the work of the compressor and turbine, where the convention is that heat received is positive and heat rejected is negative and work done is positive and work absorbed is negative.
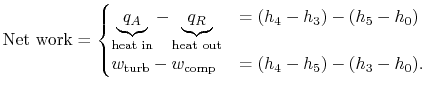 |
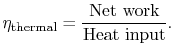
We need to calculate
From the definition of
![]() ,
,
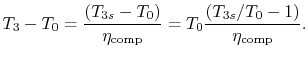
With
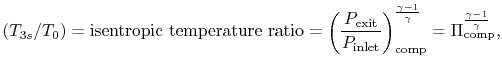
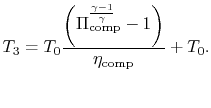
Similarly, by the definition
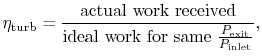
we can find
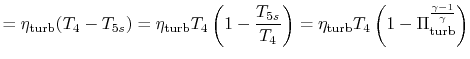 |
||
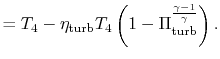 |
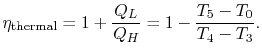
With
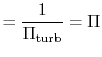 |
||
|
and
| ||
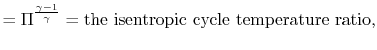 |
||
![$\displaystyle = 1-\cfrac{T_4\left[1-\eta_\textrm{turb}\left(1-\cfrac{1}{\tau_s}...
...ht)\right]-T_0} {T_4-T_0\left[\cfrac{1}{\eta_\textrm{comp}}(\tau_s-1)+1\right]}$](img1419.png) |
||
|
or
| ||
![$\displaystyle = \frac{\left[1-\cfrac{1}{\tau_s}\right]\left[\eta_\textrm{comp}\...
...0}-\tau_s\right]} {1+\eta_\textrm{comp}\left[\cfrac{T_4}{T_0}-1\right]-\tau_s}.$](img1420.png) |
||
Putting this in a non-dimensional form,
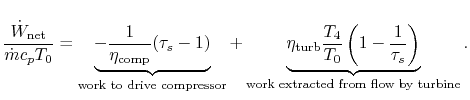
![$\displaystyle \frac{\dot{W}_\textrm{net}}{\dot{m}c_pT_0} =
(\tau_s-1)\left[\cfrac{\eta_\textrm{turb}\cfrac{T_4}{T_0}}{\tau_s}-\frac{1}{\eta_\textrm{comp}}\right]$](img1431.png)
|
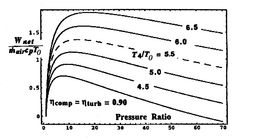
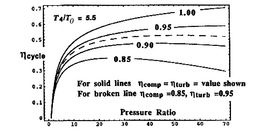
[Non-dimensional work as a function of cycle pressure ratio for
different values of turbine entry temperature divided by compressor
entry temperature]
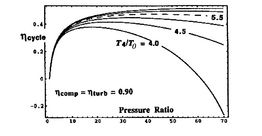
 [Overall cycle efficiency as a function of pressure ratio for
different values of turbine entry temperature divided by compressor
entry temperature]
[Overall cycle efficiency as a function of pressure ratio for
different values of turbine entry temperature divided by compressor
entry temperature]
 [Overall cycle efficiency as a function of cycle pressure
ratio for different component efficiencies]
[Overall cycle efficiency as a function of cycle pressure
ratio for different component efficiencies]
|
Trends in net power and efficiency are shown in Figure 11.20 for parameters typical of advanced civil engines. Some points to note in the figure:
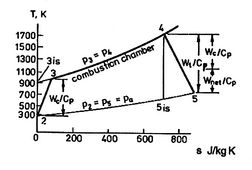
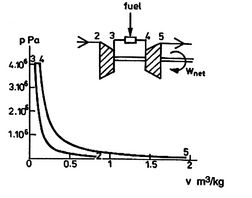
A scale diagram of a Brayton cycle with non-ideal compressor and
turbine behaviors, in terms of temperature-entropy (![]() -
-![]() ) and
pressure-volume (
) and
pressure-volume (![]() -
-![]() ) coordinates is given below as
Figure 11.21.
) coordinates is given below as
Figure 11.21.
|
[]
 []
[]
|
Muddy Points
Isn't it possible for the mixing of two gases to go from the final state to the initial state? If you have two gases in a box, they should eventually separate by density, right? (MP 11.9)
How can ![]() be the maximum turbine inlet temperature?
(MP 11.10)
be the maximum turbine inlet temperature?
(MP 11.10)
When there are losses in the turbine that shift the expansion in
![]() -
-![]() diagram to the right, does this mean there is more work than
ideal since the area is greater? (MP 11.11)
diagram to the right, does this mean there is more work than
ideal since the area is greater? (MP 11.11)
For an afterburning engine, why must the nozzle throat area increase if the temperature of the fluid is increased? (MP 11.12)
Why doesn't the pressure in the afterburner go up if heat is added? (MP 11.13)
Why is the flow in the nozzle choked? (MP 11.14)
What's the point of having a throat if it creates a retarding force? (MP 11.15)
Why isn't the stagnation temperature conserved in this steady flow? (MP 11.16)
UnifiedTP