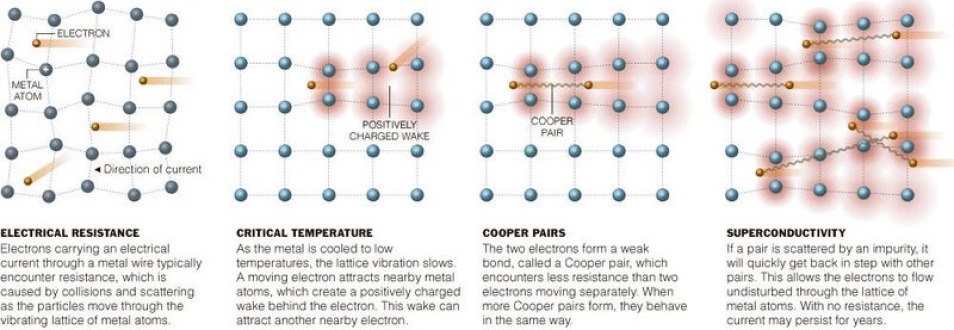
Symmetry breaking is a collective behavior of the physical system. Although one can read-off that information locally from the Lagrangian or Halmintonian of the system, but the phenomenon itself can only be realized through a collection of degrees of freedom. The simplest explanation can be seen from the following example: consider a material in superconductor phase (with the familiar gauge symmetry U(1) is broken), and take a look at a single electron. The electron itself is an gauge invariant object, and it couldn't tell whether the phase of the material breaks symmetry or not. Therefore, by definition, symmetry breaking is a collective phenomenon.
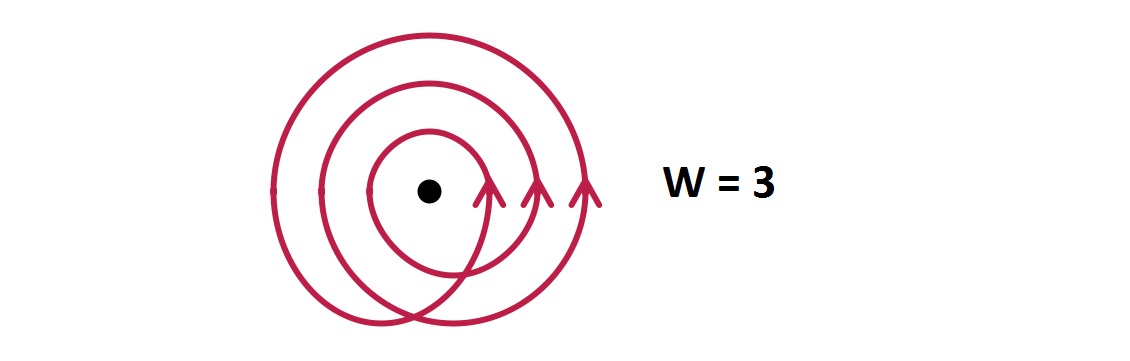
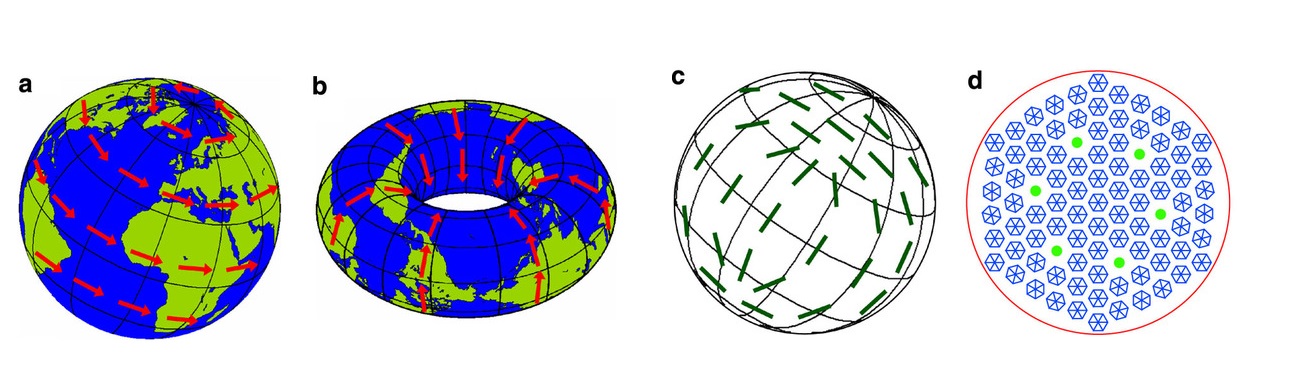
Topological defects, in a conventional sense, is a quantized object (therefore, macroscopic objects like ocean vortices or smoke rings aren't topological defects, although there are many similarities between them). It's usually the case that topological defects are a lot more stable compare to a composite object in the theory since these quantized defects are protected by the system itself (unpatchable defects), at least up to a certain energy scale - the symmetry broken scale. Symmetry breaking supports topological defects, that can be seen, but also note that most of the time, topological defects are formed only if the system has a symmetry breaking. That's not always true, since there are cases when topological defects are formed without symmetry breaking: if the spatial region is non-trial, there are topological properties arised from the geometry and stable topological objects can appear, for example a compact space can supports Kaluza-Klein type topological defect which corresponds to the winding number - the topological label for fields when one examines a loop around the compacted direction. Another example is the field value space itself is non-trivial, for example in the Ising model (as the field can only receive 2 different values)
 Without symmetry breaking, all field configurations in trivial spatial region are are topologically equivalent since each field value can locally
change to a new value without constrain. With symmetry breaking and the result order parameter space compacted, then it's straight-forward see that
quantization can naturally arise from that compactness (for example, if the order parameter space is topologically equivalent to a circle then
one can has quantized winding number, which is an integrer). This quantization structure can be read-off from homotopy
and homotopy group, associated possible topological defects with distinct labels.
Without symmetry breaking, all field configurations in trivial spatial region are are topologically equivalent since each field value can locally
change to a new value without constrain. With symmetry breaking and the result order parameter space compacted, then it's straight-forward see that
quantization can naturally arise from that compactness (for example, if the order parameter space is topologically equivalent to a circle then
one can has quantized winding number, which is an integrer). This quantization structure can be read-off from homotopy
and homotopy group, associated possible topological defects with distinct labels.