In field theory, perturbative configuration fluctuates on a fixed background is often well-understood, since the mathematical properties of the system are relatively easy (wave-behavior, order-by-order expansion, small coupling ...) and simple enough for quantization (the step from classical to quantum Physics) most of the time. Topological defects (the term "topological" here comes from the homotopical distinction betweem the theory's solution has these objects and the vacuum solution) , also known as topological soliton, are non-perturbative objects originates from the collective behaviors of fields, therefore the Physics arised are very different and extremely interesting. Let's use a simple classical example to demonstrate that: consider the air, a system of many molecules moving around rapidly. The study of perturbation behaviors of these air molecules around a static (non-moving) air flow gives the Physics of sound propagation, and if the background - the air flows with some fixed velocity (at least, inside the region of interests) then ones can learn about the Doppler effect for sound. These above topics are all well-understood. Above the realm of perturbative dynamics, one has to deal with the air movement - this topic play an important role in Atmospheric Science and weather forecast. A topological defect (actually, it's not a topological defect in a conventional sense since the defect itself is not quantized; however, for the sake of demonstration, let just assume that) results from the air movement is air vortex - storm and tornado. These objects have complicate interactions with the topography of the Earth and with themselves, and predicting their trajectories correctly is a difficult task, nearly impossible.

It's straight-forward to read-off the perturbative behaviors of a theory from its mathematical equations (the Halmintonian, the Lagrangian, the constrain equations, ..., at least most of the time. However, the non-perturbative behaviors require more works to get, and most of the robustness of the theory are lying there. Indeed, to put it in simple words, perturbative solutions to a given theory can be thought as the approximation linearize solutions to a complicate polynomial, while the non-perturbative ones correspond to the analytical solutions. Therefore, like any other non-perturbative aspects of a field theory, the Physics of topological defects is rich.
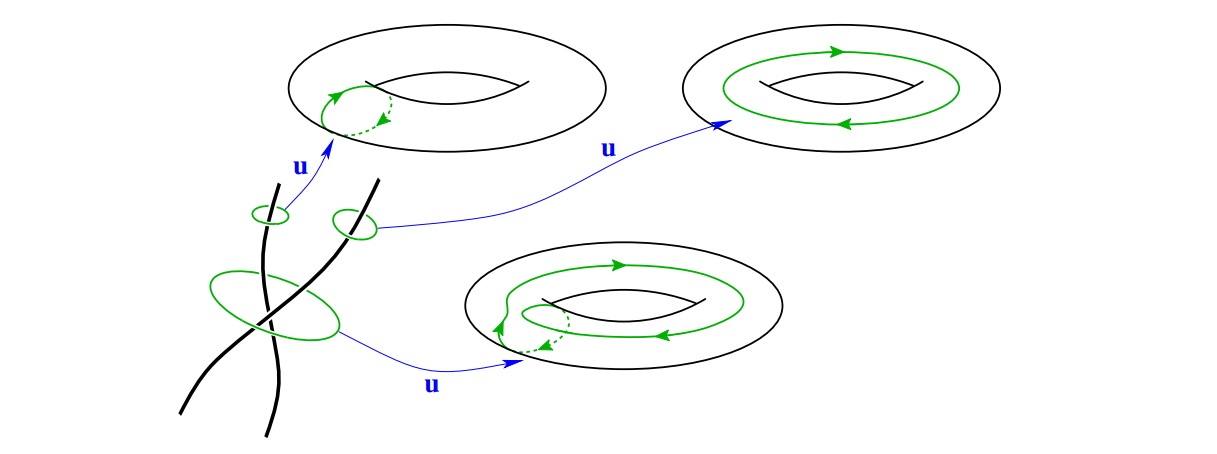
Note that, under or above a certain energy scale, length scale or a physical case, the Physics of perturbation becomes neglectable as the fundamental effective degrees of freedom (variables and fields that one can use to define the theory) becomes that of the topological defects (in rarer cases, both can still be included, but let's save that story for another time). Under the point of view of the new effective field theory, some Physics of the topological defects can be treated as perturbative while others can be used to form an even more non-perturbative object - a new composite object or a new topological defect originates from the collective behaviors of the old topological defects. And maybe so on, with the next scale and the one after, and the upper limit is depended on the type of interactions these topological defects has. An example about this is given in the below picture (the "first" topological defects are vortices, and two of themselves can be bound together and create another point particle - a composite object), which you can read more about it in another part of this Website:

For a quick mathematical introduction to topological defects, you can read it in another part of this Website