Fractals
On this last page, we will discuss fractals and see in which way the models for random surface growth are fractal. The references give further reading for the interested student (or teacher)!
In all the models for random growth that we saw on the last page, the surface of the random system was very tree-like, branching into different directions. In mathematics, these objects are said to be fractal - which means more than just being treelike. A fractal is a system that is self-similar, i.e. it has the same appearance, no matter how far you zoom in, and is very commonly found in nature. Some examples of this includes all the pictures in the introduction and river networks, tree branches, coastlines and even mountain goat horns!
An example we can analyze a little more is given by Brownian motion: after zooming in on the Brownian motion, it is impossible to tell if you are looking at the original image or the zoomed in version, as shown in the following animation:
Zooming in on the trajectory of a Brownian motion
Fractal dimension
There are more examples of fractals - some of them will be more winding than others, occupying more space than others, and we would like to be able to measure this ‘bigness’. One way of doing that is through the concept of fractal dimension. As an example, consider the following classical example - measuring the coast length of Great Britain. Using a long length-stick (say one of a couple hundred miles), you would measure one yard-stick length between London and Wales, and one between Wales and Scotland, and another one between Scotland and London, so we would arrive at a total length of 3 length-sticks. Now, if we start with a yard-stick of half that length, we can measure more of the nooks and crannies in the coast-line, so might end up with a total length of 8 of these new length-sticks. This means that the second measurement gives a length significantly larger than the first one! This comes from the fractal nature of the coast-line and is what we will explore now.
Box-counting dimension of the coast of Britain
We will quantify this by defining the box-counting dimension of a fractal. To measure how big it is, we cover it by the smallest number of boxes of side-length \(\varepsilon\) that we need to cover it. If we denote this number by \(N(\varepsilon)\), then we can measure \(N(\varepsilon)\) for a number of smaller and smaller \(\varepsilon\).
Exercise: box-counting.
a): Calculate \(N(\varepsilon)\) for a straight line of length \(L\) in one dimension and \(\varepsilon = L, \frac{L}{2}, \frac{L}{3}.\)
b): Calculate \(N(\varepsilon)\) for a square of sides \(L\times L\) in two dimensions and \(\varepsilon = L, \frac{L}{2}, \frac{L}{3}.\)
c): Calculate \(N(\varepsilon)\) for a cube of sides \(L\times L\times L\) in three dimensions and \(\varepsilon = L, \frac{L}{2}, \frac{L}{3}.\)
d): From these examples, what do you think \(N(\varepsilon)\) looks like for a cube in \(D\) dimensions?
From the previous exercise, a square in \(D\) dimensions has \(N(\varepsilon)\) proportional to \(\varepsilon ^{-D}\), which we can rearrange to give \(D = -\frac{\log{N(\varepsilon)}}{\log{(\varepsilon)}}\). We can therefore recover the dimension of a square by looking at \(N(\varepsilon)\) in the right way! In the same way, we define the fractal dimension of a fractal to be \(\lim_{\varepsilon \rightarrow 0} -\frac{\log{N(\varepsilon)}}{\log{(\varepsilon)}}.\)
Exercise: fractal dimensions.
We will calculate the dimension of an interesting fractal, called the Cantor middle-thirds set which is shown in the figure below.

Cantor middle-thirds set
It is constructed in the following way. Start with a straight line of length \(1\). Divide this up into three equal segments, and remove the middle one. You are now left with two intervals of length \(1/3\), and for each of these, divide them up into three segments of equal length, and remove the third one. Continue this until the length of the smallest segment is one pixel.
What is the fractal dimension of the Cantor-middle thirds set?
Hint: if you have a stick of length \(1/3\), then after having removed the first middle set, you will always need two sticks to cover the set. What about a stick of length \(1/9\)? \(1/27\)? Use this to get to the answer!
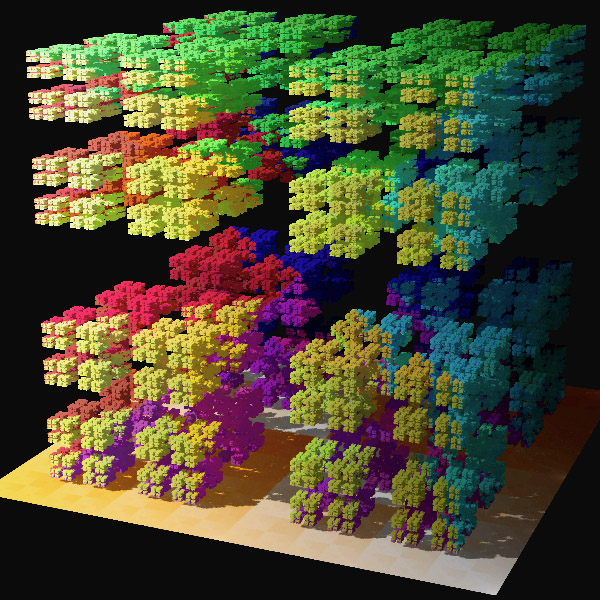
A 3D version of the Cantor middle thirds set
Fractal dimensions of random growth models
Now, we can come back to the random growth models we studied on the previous page. As we observed there, the random growth model are fractal, either because of their treelike structure (for diffusion limited aggregation) or because the boundary of the surface is very rough (Eden-Richardson growth model and KPZ equation). One way of measuring the level of fractality for these models is by looking at their fractal dimension, and scientists have done this through simulations and from deriving exact formulas. This has resulted in the following table:
| Model | Fractal dimension |
| Diffusion limited aggregation (2D) | 1.71 |
| Eden-Richardson (2D) | 1.5 |
| Eden-Richardson (3D) | 1.6-1.8 |
| KPZ (2D) | 1.5 |
| KPZ (3D) | 1.6-1.8 |
Further reading:
A fun experiment to create your own fractals: Science Buddies, de Brabandere, ‘‘Mesmerizing Fractals’’, https://www.scientificamerican.com/article/mesmerizing-fractals/.
Mandelbrot, ‘‘How Fractals Can Explain What's Wrong with Wall Street’’, https://www.scientificamerican.com/article/multifractals-explain-wall-street/.
Mandelbrot, and Pignoni. ‘‘The fractal geometry of nature.’’ (1983).