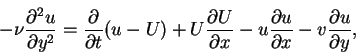Momentum Integral

Next: Energy Integral. Up: Momentum and Energy Equations. Previous: Momentum and Energy Equations.

Momentum Integral

We can write equation (4.77) in the form

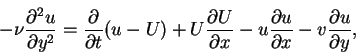$\begin{displaymath}-\nu\frac{\partial^{2}u}{\partial y^{2}} = \frac{\partial}{\p... ...u\frac{\partial u}{\partial x}-v\frac{\partial u}{\partial y}, \end{displaymath}$

(89)

and if we multiply equation (4.78) by (u-U) we obtain

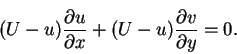$\begin{displaymath}(U-u)\frac{\partial u}{\partial x}+(U-u)\frac{\partial v}{\partial y} = 0. \end{displaymath}$

(90)

If we add these two equations, we obtain

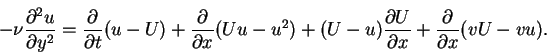$\begin{displaymath}-\nu\frac{\partial^{2}u}{\partial y^{2}} = \frac{\partial}{\p... ...ac{\partial U}{\partial x}+\frac{\partial}{\partial x}(vU-vu). \end{displaymath}$

(91)

Next, we integrate with respect to y from 0 to 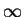$\infty$ . This yields

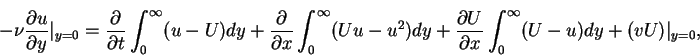$\begin{displaymath}-\nu\frac{\partial u}{\partial y}\vert _{y=0} = \frac{\partia... ...rtial U}{\partial x}\int_{0}^{\infty}(U-u)dy+(vU)\vert _{y=0}, \end{displaymath}$

(92)

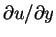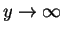since $\partial u/\partial y$ and v(U-u) tend to zero as $y\rightarrow \infty$ . If there is no suction at the body surface, v_y=0 = 0. We assume that there is no suction at the body surface, and by taking into account equations (4.79) to (4.82), we can write equation (5.92) in the form

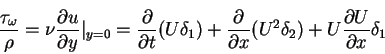$\begin{displaymath}\frac{\tau_{\omega}}{\rho} = \nu\frac{\partial u}{\partial y}... ...l x}(U^{2}\delta_{2})+U\frac{\partial U}{\partial x}\delta_{1} \end{displaymath}$

(93)

Next: Energy Integral. Up: Momentum and Energy Equations. Previous: Momentum and Energy Equations.

Karl P Burr
2003-03-12