| Vol.
XX No.
4 March / April 2008 |
| contents |
| Printable Version |
Teach Talk
Skills, Big Ideas, and Getting Grades Out of the Way
“What was class average?” I feel like I have been asked a 1,000 times, and I confess, each time it makes me cringe. It tells me the student is fixated on evaluation, not on the material. It tells me the student is competing with other students, rather than aspiring for a level of knowledge. It tells me the student thinks we grade on a curve, which is prohibited by a sensible MIT rule. And worst of all, it tells me the student is focusing on testable skills that can be taught anywhere, not on absorbing the big ideas that can only be taught at a place that develops big ideas.
In the fall of 2006, just after yet another student in 6.034, Introduction to Artificial Intelligence, asked the class-average question, we of the staff decided that we had had enough, and that it was time to start over in a search for a better way of certifying skills. Our first step was to enumerate some principles:
- We should find a way to deemphasize grades so as to make room for big ideas
- We should test understanding, not speed and general intelligence
- We should not care whether a student demonstrates understanding early in the semester, or late, as long as the student demonstrates understanding.
- We should give an A to every student that demonstrates A-level understanding
Guided by our desire to test subject understanding and deemphasize quiz-taking speed, we decided to move from two material-packed quizzes to four more relaxed quizzes. Further guided by our desire to test subject understanding rather than general intelligence, we decided to resist the temptation to be so clever that our quizzes test the students on how well they can penetrate our cleverness, rather than their understanding of the material.
To acknowledge that we do not care when a student demonstrates subject understanding, as long as the student demonstrates understanding, we decided to divide our final examination into parts corresponding to the four quizzes, plus a fifth part covering material taught after the latest quiz date that Institute rules allow. Then, we award the student the higher of the grades they get on the quizzes and the corresponding parts of the final.
This maximizing created a minor problem because a good numerical score on a particular quiz might be substantially higher or lower than a good grade on the corresponding part of the final, so we had to devise a way to decide which score was better and a way to combine that better score into a final-grade formula.
We could have just normalized the means and standard deviations, but that distribution-oriented approach seemed inconsistent with our antibodies against the “What was class average?” question.
Accordingly, we decided to transform each 0–100 numerical quiz score into an integer from 3 to 5. For each quiz, we decided on a threshold for thorough understanding, and each student who scores above that threshold comes away with a 5. Each student who scores lower than that but above our adequate understanding threshold, earns a 4. Lower than that but above our needs work threshold gets a 3. Lower than that, we award only 0, 1, or 2, depending on how much lower.
This thresholding scheme has two virtues. First, we solve the problem of deciding whether the quiz score is higher or lower than the corresponding part of the final. Second, there is far less grade grubbing because there is no point in arguing about a few points when a student's grade is more than a few points shy of the next threshold.
Better yet, when a student asks the class-average question, we are able to say, with pride, “We have no idea.” They soon quit asking.
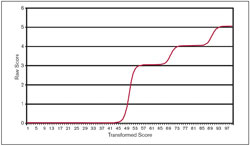
To diminish grade grubbing when grades fall near thresholds, we added to our grade-recording spreadsheet a smoothed staircase function that transitions rapidly near the thresholds, rather than with a singularity. The function was borrowed from neural-net learning theory:

where the G is the transformed grade; s is the raw score; the ts are the thresholds; and c is a constant that determines the degree of smoothing. We found c = 0.7 to be about right, producing the graph shown for thresholds at 50, 70, and 90:
At the end of the subject, we are left with six numbers from 0 to 5: four are the results of maximizing quiz scores and final scores; one comes from the fifth part of the final; the sixth comes from homework and a subjective assessment of class participation. If the average is 4.5 or better, the student gets an A; 3.5–4.5, a B; 2.5–3.5, a C; and every student below 2.5 is the subject of a full discussion. Thus, there is a kind of 6.034 GPA that determines each student's final grade.
The students love our grading procedure because they get two shots at each chunk of material. Also, they know that if they are content with a quiz score, they need not do the corresponding part of the final at all, so they can focus their preparation for the final on precisely the subject matter that needs the most work.
When we first tried our new grading procedure in the fall of 2006, we expected many students to leave by the end of the first hour or two of our three-hour final, because there were a substantial number who were in the highest category for all or all but one of the four quizzes. As time went by, we noted, with some alarm, that many known-to-be-excellent students stayed the entire three hours. When the exam was over, we asked one of the highest-category students why she did all five parts when we had made it clear she needed to do only one. “Oh,” she said, “I did the rest for fun!” Our pride was palpable. We knew we were on to something.
| Back to top | |
| Send your comments |
| home this issue archives editorial board contact us faculty website |