User’s Guide, Chapter 7: Chords¶
Chords, as the name might suggest, are objects that combine multiple
Pitch objects on a single stem. They can be
found in the music21.chord module. The most general way to create
a Chord object is by passing in a list of
pitch names you want in the chord:
from music21 import *
cMinor = chord.Chord(["C4","G4","E-5"])
Note and Chord objects, since both are subclasses of the
GeneralNote object share many features in
common:
cMinor.duration.type = 'half'
cMinor.quarterLength
2.0
But since a Chord contains many pitches, it does not have a
.pitch attribute:
cMinor.pitch
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
<ipython-input-3-e8314cc72a18> in <module>
----> 1 cMinor.pitch
AttributeError: 'Chord' object has no attribute 'pitch'
Instead it has a .pitches
attribute which returns a Tuple of pitches in the Chord.
cMinor.pitches
(<music21.pitch.Pitch C4>, <music21.pitch.Pitch G4>, <music21.pitch.Pitch E-5>)
A little bit more about Python. .pitches returns a tuple, what’s
that? A tuple is like a list, except that unlike a list which has square
brackets around it, a tuple has parentheses around it:
baroqueTuple = ('Strozzi', 'Bach', 'Handel', 'Telemann')
classicalList = ['Mozart', 'Haydn', 'Saint-George', 'Beethoven']
baroqueTuple
('Strozzi', 'Bach', 'Handel', 'Telemann')
classicalList
['Mozart', 'Haydn', 'Saint-George', 'Beethoven']
Both tuples and lists can find members by accessing them with numbers in square brackets:
baroqueTuple[0]
'Strozzi'
classicalList[0]
'Mozart'
But the biggest difference between the two is that you can manipulate a
list, but not a tuple. If we try to add someone to the classicalList,
using .append it works great.
classicalList.append('Ella Fitzgerald') # she's a classic to me...
classicalList
['Mozart', 'Haydn', 'Saint-George', 'Beethoven', 'Ella Fitzgerald']
classicalList.remove('Mozart')
classicalList
['Haydn', 'Saint-George', 'Beethoven', 'Ella Fitzgerald']
But a tuple can’t be changed:
baroqueTuple.append('Miles Davis')
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
<ipython-input-17-fd7e965db659> in <module>
----> 1 baroqueTuple.append('Miles Davis')
AttributeError: 'tuple' object has no attribute 'append'
In this case, that’s a shame, because Miles belongs with Bach! So we shouldn’t have used a tuple there.
But in the class of .pitches it makes sense that it returns a tuple,
since changing the result .pitches separate from the Chord could be
ambiguous – did you mean to change the result of .pitches or to
change the pitches in the chord itself? music21 will often return
tuples in places where manipulating the result could cause headaches or
bugs down the line. In any case, it’s easy to turn a tuple into a list
or vice versa:
baroqueList = list(baroqueTuple)
baroqueList.append('Miles Davis')
baroqueList
['Strozzi', 'Bach', 'Handel', 'Telemann', 'Miles Davis']
classicalTuple = tuple(classicalList)
classicalTuple
('Haydn', 'Saint-George', 'Beethoven', 'Ella Fitzgerald')
Okay, back to chord, where we left off:
cMinor.pitches
(<music21.pitch.Pitch C4>, <music21.pitch.Pitch G4>, <music21.pitch.Pitch E-5>)
But you already knew what pitches were in the Chord since you just
created it! What else can you do with it?
How about determining if it is a
major or a
minor triad?
cMinor.isMajorTriad()
False
cMinor.isMinorTriad()
True
You can also figure out if it is in inversion or not:
cMinor.inversion()
0
Chords in root position have inversion of 0. But consider this other chord:
cMajor = chord.Chord(["E3","C4","G4"])
cMajor.inversion()
1
With this chord, two other methods become important:
cMajor.root()
<music21.pitch.Pitch C4>
cMajor.bass()
<music21.pitch.Pitch E3>
You can find the third and fifth of the Chord with .third and
.fifth. Note that these properties do not have () after them. This
was a mistake in how we created music21 and hopefully this will all
be fixed and consistent soon:
cMajor.third
<music21.pitch.Pitch E3>
cMajor.fifth
<music21.pitch.Pitch G4>
There is also a .seventh property, but it won’t do anything here:
cMajor.seventh
The result of that is None which we can test like so…
cMajor.seventh is None
True
We can append or remove notes from a chord, just like in a set:
dMaj = chord.Chord('D4 F#4')
dMaj.add('A5')
dMaj
<music21.chord.Chord D4 F#4 A5>
dMaj.remove('D4')
dMaj
<music21.chord.Chord F#4 A5>
dMaj.add(pitch.Pitch('D3'))
dMaj.add(note.Note('F#5'))
dMaj
<music21.chord.Chord D3 F#4 F#5 A5>
Displaying Chords¶
We can display the Chord object just like any
Note (Don’t worry if this isn’t working for you
yet…we’ll get this set up in Chapter 8)
cMinor.show()
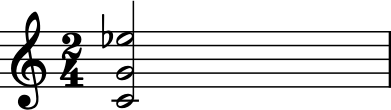
cMajor.show()

These chords are a bit “spacey”, so let’s get c in
closedPosition():
cClosed = cMinor.closedPosition()
cClosed.show()

Notice that cMinor is unchanged. The closed position chord is only
cClosed:
cMinor.show()
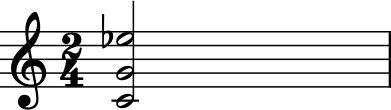
If we wanted to change the Chord object itself, we call
.closedPosition(inPlace=True) which alters the original. Since the
original is altered, we don’t put x = ... in front of it.
cMajor.closedPosition(inPlace=True)
cMajor.show()

There is also a method,
semiClosedPosition() which acts like
.closedPosition except that if there is already a pitch at that step
(i.e., D-flat and D-sharp are both step “D”), then the note is moved up
an octave. This is useful for displaying complex, post tonal chords in
the most compact form possible:
c1 = chord.Chord(['C4', 'E5', 'C#6', 'E-7', 'G8', 'C9', 'E#9'])
c2 = c1.semiClosedPosition()
c2.show()

We can get the common name of
each of these Chords:
cn1 = cMinor.commonName
print(cn1)
minor triad
print(cMajor.commonName)
major triad
More complex chords have less common “commonNames”. Here’s one that the American composer Elliott Carter liked a lot.
elliottCarterChord = chord.Chord(['C4','D-4','E4','F#4'])
elliottCarterChord.commonName
'all-interval tetrachord'
elliottCarterChord.show()

More ways of creating chords; Chords and Streams¶
There are other ways of creating a Chord if you’d like. One way is from
a bunch of already created Note objects:
d = note.Note('D4')
fSharp = note.Note('F#4')
a = note.Note('A5')
dMajor = chord.Chord([d, fSharp, a])
dMajor.show()

Or we can pass a string with note names separated by spaces:
e7 = chord.Chord("E4 G#4 B4 D5")
e7.show()
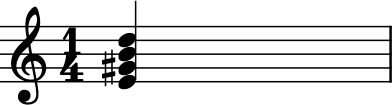
The octaves are optional, especially if everything is within an octave:
es = chord.Chord("E- G B-")
es.show()

But you will definitely want them if a chord crosses the boundary of an octave (between B and C). Unless you love 6-4 chords, this is probably not what you want:
fMajor = chord.Chord("F A C")
fMajor.show()

Notice that because C sorts before F and A that the chord is in second
inversion, or 64. We can figure out the inversion of a Chord like
so:
print(fMajor.inversion(), fMajor.inversionName())
2 64
In addition to .commonName, there are a few other “name” properties that might be interesting:
fMajor.fullName
'Chord {F | A | C} Quarter'
fMajor.pitchedCommonName
'F-major triad'
Like Note objects, we can put Chord objects inside a
Stream:
stream1 = stream.Stream()
stream1.append(cMinor)
stream1.append(fMajor)
stream1.append(es)
stream1.show()

We can mix and match Notes, Rests,
and Chords:
rest1 = note.Rest()
rest1.quarterLength = 0.5
noteASharp = note.Note('A#5')
noteASharp.quarterLength = 1.5
stream2 = stream.Stream()
stream2.append(cMinor)
stream2.append(rest1)
stream2.append(noteASharp)
stream2.show()

Post-tonal chords (in brief)¶
There are a lot of methods for dealing with post-tonal aspects of chords. If you’re not interested in twentieth century music, go ahead and skip to the next chapter, but, here are some fun things.
The intervalVector of a chord is a list of the number of
[semitones, whole-tones, minor-thirds/augmented-seconds, major-thirds, perfect fourths, and tritones]
in the chord or inversion. A minor triad, for instance, has one minor
third (C to E-flat), one major third (E-flat to G), and one perfect
fourth (G to C above, since octave does not matter):
cMinor.intervalVector
[0, 0, 1, 1, 1, 0]
A major triad has the same interval vector:
cMajor.intervalVector
[0, 0, 1, 1, 1, 0]
The elliottCarterChord is unique in that it has an .intervalVector
of all 1’s:
elliottCarterChord.intervalVector
[1, 1, 1, 1, 1, 1]
Well, it’s almost unique: there is another chord with the same
.intervalVector. That Chord is called its Z-relation or Z-pair.
elliottCarterChord.hasZRelation
True
otherECChord = elliottCarterChord.getZRelation()
otherECChord
<music21.chord.Chord C D- E- G>
otherECChord.show()

otherECChord.intervalVector
[1, 1, 1, 1, 1, 1]
The other post-tonal tools you might be interested in are given below. We’ll return to them in a later chapter, but here are three important ones:
print(elliottCarterChord.primeForm)
[0, 1, 4, 6]
print(elliottCarterChord.normalOrder)
[0, 1, 4, 6]
print(elliottCarterChord.forteClass)
4-15A
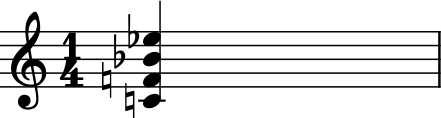
If you really only care about semitones, you can create a chord just with the pitchClasses:
oddChord = chord.Chord([1, 3, 7, 9, 10])
oddChord.show()

There’s a little problem with the A and A# being on the same space that makes it hard to read. Let’s flip the A# to Bb:
oddChord.pitches[-1].getHigherEnharmonic(inPlace=True)
oddChord.show()

If you use pitchClasses above 11, then they are treated as MIDI numbers, where 60 = MiddleC, 72 = C5, etc. Enharmonic spelling is chosen automatically.
midiChordType = chord.Chord([60, 65, 70, 75])
midiChordType.show()
Okay, so now you’ve learned the basics (and more!) of Notes and Chords.
If you haven’t been able to see them on your own,
Chapter 8: Installing MusicXML Readers
will fix it. It’s also going to cover the basic file formats of
music21.