5) Soap bubbles and detergents...
How do soap bubbles form? Why does soapy water produce foam while pure water does not? Scroll below to find some answers....
(i) Bubbles in soap films but not in water...
 |  |
Click here for the video: No bubbles in water, Bubbles in soapwater
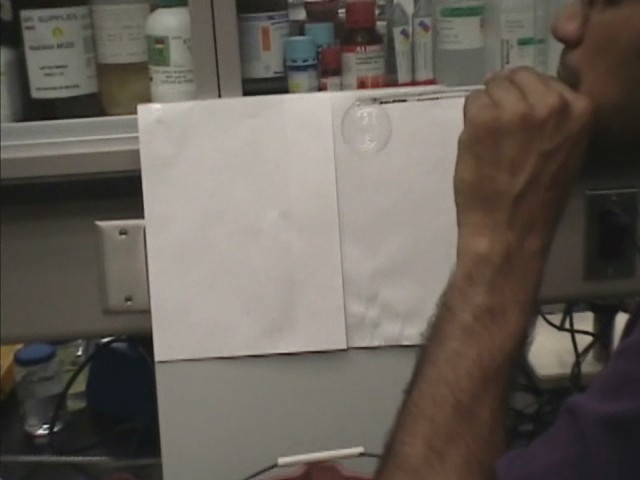
When water sprays from a tap in a small basin, you can see bubbles form, but they burst very soon. This is due to the fact that the surface tension of the normal water is high and it tends to draw the water molecules into the main body of the water., to the point where the thickness of the bubble wall is too thin to remain intact and quickly bursts. Instead, the surface tension of the soapy water is much lower: about a third of the pure water, and so the molecules of the bubble are less stressed and it can last longer.
(ii) Soap bubbles...
 |
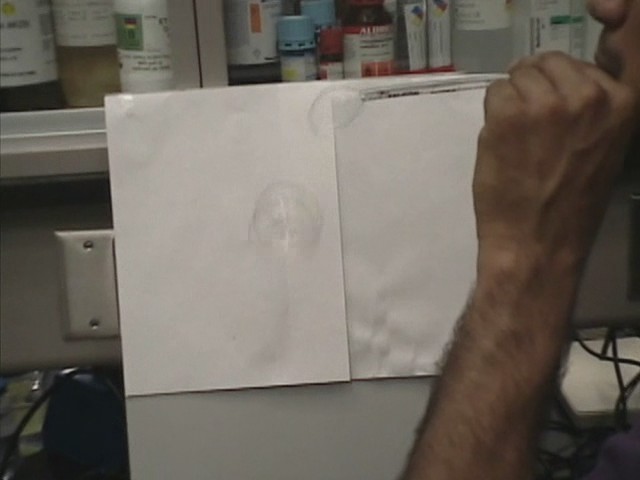 |
Soap bubbles can be formed with "soapy" water, which can be very stable and can fly!
(iii) Large soap bubbles...
 |  |
 |
Δ p = pinside - poutside = (4γ ) / R
As one passes across a curved surface or interface, a jump in pressure occurs given by above relationship. (R is the radius of curvature of the surface, γ is the surface tension. The smaller the drop, therefore, the greater its internal pressure. In the above case, the radius of curvature for the smaller and larger bubbles are 3 cm and 9 cm respectively. Hence the pressure in the smaller bubble would be higher in comparison to the pressure inside the larger bubble. The excess pressure in the larger bubble would be ~1 N/m2 and in the smaller bubble would be ~3 N/m2.
(iv) Foam
 |
Foam is created when the surface tension of water (attraction of surface molecules toward the center, which gives a drop of water its round shape) is reduced and air is mixed in, causing bubble formulation.
(v) Laplace Pressure
As one passes across a curved surface or interface, a jump in pressure occurs. The smaller the drop, the greater is its inner pressure. Surface tension is at the origin of the overpressure existing in the interior of drops and bubbles.
Δ p = pinside - poutside = γ (1/ R + 1/R') = γ C
The increase in hydrostatic pressure Δ p that occurs upon traversing the boundary between two fluids is equal to the product of the surface tension γ and the curvature of the surface C= (1/ R + 1/R'), where R and R' are the radii of curvature of the surface. For a sphere, R=R'.
Δ p = pinside - poutside = (2 γ ) / R
 |
 |
 |
(vi) Contact interface between equal-size and unequal-size bubbles
 |
 |
| equal-radii bubbles | unequal-radii bubbles |
Click here for the videos: equal-radii bubbles, unequal-radii bubbles
When bubbles of different radii come in contact with each other, internal surfaces will be curved. This is due to the pressure difference between neighboring bubbles (see discussion on Laplace pressure above). Bubbles of equal radii will have the common internal surface with zero curvature. The shape of the interface in this case will be a disc.
(vii) Symmetry in bubble contact-lines
 |
At a point where two or more bubbles meet, they sort themselves out so that
only three bubble walls meet along a line, separated by angles of 120°.
This is the most efficient choice, again, which is also the reason why the cells
of a beehive use the same 120° angle, thus forming hexagons. Only four bubble
walls can meet at a point, with the lines where triplets of bubble walls meet
separated by 109.47°.
(viii) Practical consequences:
- Inflation of lungs at birth initiated by surfactant molecules that lower the surface energy of the lungs. In some premature babies, these molecules are missing and the lungs are not ready to function on their own. This respiratory stress syndrome, known as hyaline membrane disease, is alleviated by the swift delivery of suitable surfactants. For more information about mechanism of pulmonary surfactant, click here.
-blowing a balloon
-small bubbles empty themselves into larger ones.
-smaller drops will disappear in favor of larger ones in an emulsion, and they will be the first to evaporate during the cooling phase of an aerosol.
- explains the phenomenon of capillary adhesion between two plates, between hairs or fibres, or in wet sand, all of which are induced by capillary bridges.
(demo coming soon....)
Back to index ||Introduction to surface tension ||Definition of surface tension||Interfacial tension ||Minimal surfaces ||Soap bubbles, Surfactants and Detergents
Wettability||Role of roughness ||Capillarity and gravity||Dynamical effects and instability||Special interfaces ||Current research in wettability
Back to NIRT Home||On our current research ||More on Wetting||Contact Angle Measurement||Atomic Force Microscopy ||My personal homepage