4) Examples of Minimal Surfaces
Since, when segregated to the surface, a liquid molecule is in an unfavorable energy state, liquid evolves spontaneously so as to minimize its surface area.
(i) Shape of a string supporting a film...
 |  |
 |  |
Imagine a rigid metal frame bent in the form of a wedge and its two extremities connected by a thin sewing thread. If one deposits a liquid film (such as soap film) within the wedge, the film will want to shrink its surface area. As it does so, it pulls perpendicularly and uniformly on every element of the thread, which will ultimately lose its slack and take on the shape of a taut circular arc.
(ii) Loop stretching into a circle...
 |  |
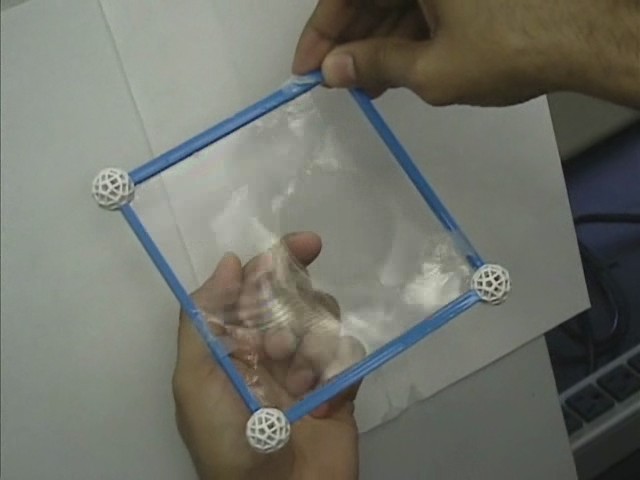 |  |
A flexible loop, secured by two threads to the frame, is embedded in the membrane. The loop is free to take on any shape until the membrane is punctured, at which time the loop stretches into a circle.
(iii) To cross a membrane without bursting it...
 |  |
 |
 |
 |
If you touch a film with a dry finger, the membrane will burst. If you will wet the same finger with the soapy solution, the film will not burst and you will be able to penetrate it.
(iv) Soap films on various shapes and structures
A soap film contained by any fixed boundary will acquire its minimum free energy when it reaches equilibrium. As the free energy of a film is proportional to its area, the area will also be minimized. Consequently soap films can be used to solve mathematical problems requiring the minimization of a surface area contained by a boundary. In order to obtain analogue solutions, we require a frame to form the boundary of the surface. When the frame is withdrawn from a bath of a soap solution a soap film will form which will attain its minimum area configuration on reaching to equilibrium.
Joseph Plateau discovered experimentally, over a hundred years ago, that soap films contained by a framework always stratify three geometrical conditions:
1) Three smooth surfaces of a soap film intersect along a line
2) The angle between any two tangent planes to the intersecting surfaces, at
any point along the line of intersection of three surfaces, is 120°.
3) Four of the lines, each formed by the intersection of three surfaces, meet
at a point and the angle between any pair of adjacent lines is 109°
28'
Tetrahedron
 |
The surface consists of six planar surfaces, each being in the shape of the isosceles triangle and bounded by an edge of the tetrahedron. All the surfaces meet at the center of the tetrahedron. Each of the two internal edges of a triangular section of soap film is joined to two other surfaces. The four lines of soap film form the internal edges of the triangular surfaces, and each line connects a vertex of the tetrahedron to its center. The lines are each formed by the intersection of three triangular planes of the soap film. The angle between adjacent sections of film is 120°. The angle between any two lines can be calculated from this information to be 109°28'.
Cube
 |  |
The minimum surface formed by dipping a cubic framework into the bath of a soap solution contains a 'square' surface at the center. The 'square' has four curved sides formed by lines of soap film that arise from the intersection of three surfaces. The curved sides of the 'square' intersect at 109° 28', as predicted by Plateau's results. There are also two other lines of film that meet at each corner of the 'square' at the angles predicted by Plateau. From the edges and corners of the 'square' are surfaces which terminate on the twelve edges of the cube. They are not all planar. The only planar surfaces are those from the vertices of the 'square' to the edges of the framework that are perpendicular to the square.
Upon rupturing one surface in cubic structure
By breaking the square at the center with finger, the minimum surface shown in following figure is obtained.
 |
It is a minimum area surfaces bounded by all twelve edges of the cube.
For a detailed discussion on minimum surfaces in three dimensions, please refer to The science of soap films and bubbles by Cyril Isenberg, Dover, 1992.
Back to index ||Introduction to surface tension ||Definition of surface tension||Interfacial tension ||Minimal surfaces ||Soap bubbles, Surfactants and Detergents
Wettability||Role of roughness ||Capillarity and gravity||Dynamical effects and instability||Special interfaces ||Current research in wettability
Back to NIRT Home||On our current research ||More on Wetting||Contact Angle Measurement||Atomic Force Microscopy ||My personal homepage