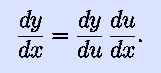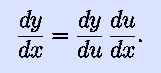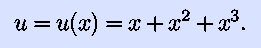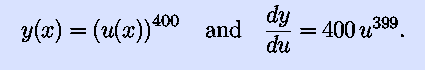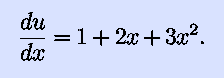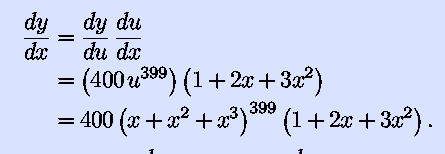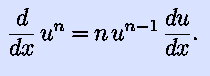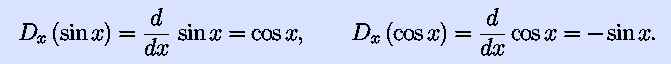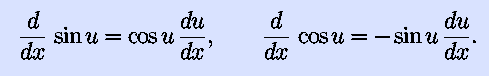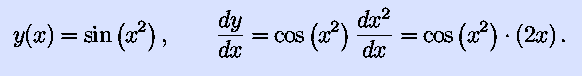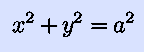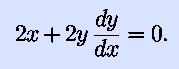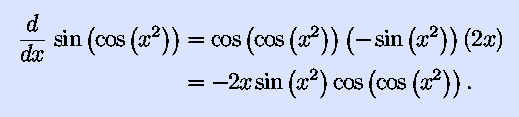Unit 3 : Trigonometry and the Chain Rule

The chain rule is the most complex of the differentiation procedures. It is also the most powerful: with it you will be able to differentiate any algebraic function. By a trick of notation, it looks innocuous enough:

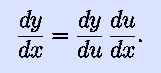Just cancel the du s. It should be stressed that this is a trick of the notation; the chain rule is actually something that needs to be proven.

The chain rule allows us to expand our previous, rather limited, power rule. Let us say we want to differentiate

without multiplying the entire mess out. Let's introduce a ``dummy'' (a fancier term is ``auxiliary'') variable,

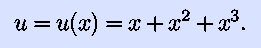We now have

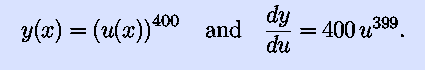We can also calculate

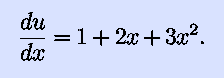The chain rule then gives

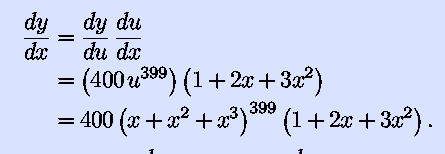A messy answer, true, but an answer we can get. Thus, our new and improved power rule is

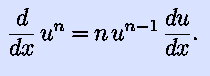Note that this contains our old power rule as the special case u=x, in which case dy/dx=1. In this unit's reading, the power rule is extended to take care of any rational n. We'll extend it to all real n eventually.

So that we have plenty of functions to differentiate, we also introduce the derivatives of the trigonometric functions this unit:

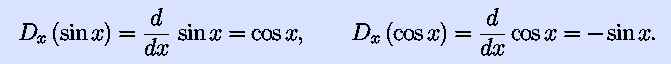The chain rule expands these to

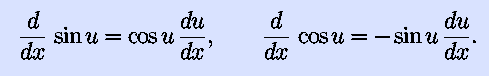For example, for

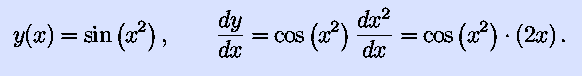
One final part of this unit is implicit differentiation: we want dy/dx, but we don't have y expressed as a function of x. For example, the equation that represents a circle of radius a in the x-y plane is

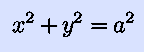where a is a constant. Implicit differentiation is simple: just take derivatives of every term:

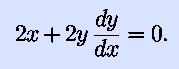(In the above, a² is a constant, so its derivative is zero.) We can then solve to get

This unit contains several new concepts. Now is the time to master them. A few pointers to help you in doing so:

Remember the du/dx tacked onto the end of the power rule and the trig rules.
When functions are deeply nested within each other, you aren't through differentiating until you've gone all the way to the inside. For example,
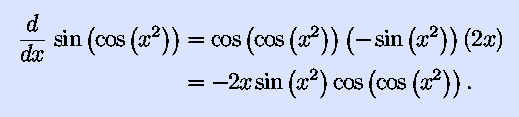
When doing implicit differentiation, remember to differentiate both sides of the equation.

Objectives:

After completing this unit you should be able to

Differentiate trig functions.

Use the chain rule to differentiate composite functions.

Use implicit differentiation to find derivatives of implicitly defined functions.

Suggested Procedure:

Read Simmons 3.3 - 3.5, 9.1, 9.2, 9.4
Read World Web Math Pages
Work lots of problems. The specific problems don't matter, but you need to work enough of these things to be able to differentiate in your sleep. Problems are located in Simmons:
- 3.3 : #1-6
- 3.4 : #1-8
- 3.5 : #1-12
- 9.2 : #1-14, 19-43 (chose a few)
- 9.4 : #1-8
- 9.5 : #4-12
Take the Practice Unit Test, Xdvi or PDF.
Ask your instructor for a unit test.
Independent Study page | Calculus page | World Web Math Categories Page

watko@mit.edu
Last Modified July 31, 1998