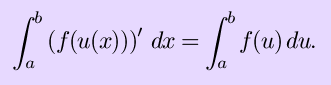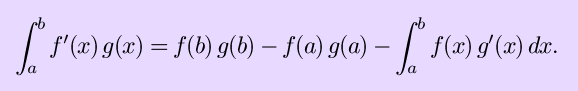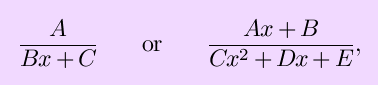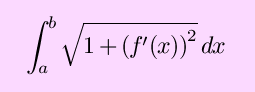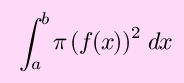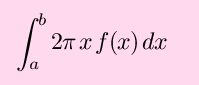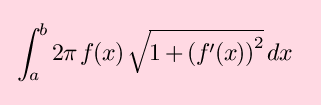Calculus Summary

Calculus has two main parts: differential calculus and integral calculus. Differential calculus studies the derivative and integral calculus studies (surprise!) the integral. The derivative and integral are linked in that they are both defined via the concept of the limit: they are inverse operations of each other (a fact sometimes known as the fundamental theorem of calculus): and they are both fundamental to much of modern science as we know it.

Derivatives

The limit of a function f(x) as x approaches a is equal to b if for every desired closeness to b, you can find a small interval around (but not including) a that acheives that closeness when mapped by f. Limits give us a firm mathematical basis on which to examine both the infinite and the infinitesmial. They are also easy to handle algebraically:

where in the last equation, c is a constant and in the first two equations, if both limits of f and g exist.

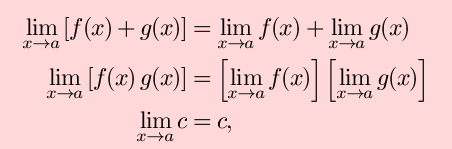
One important fact to keep in mind is that

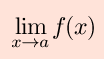
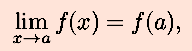
doesn't depend at all on f(a) -- in fact, f(a) is frequently undefined. In the happy case where

we say that f is continuous at a. It is also sometimes useful to talk about one-sided (left or right) limits, where we only care about the values of x that are less than or greater than a.

The derivative of f(x) at x=a (or f´(a) ) is defined as

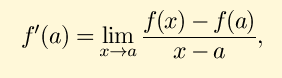
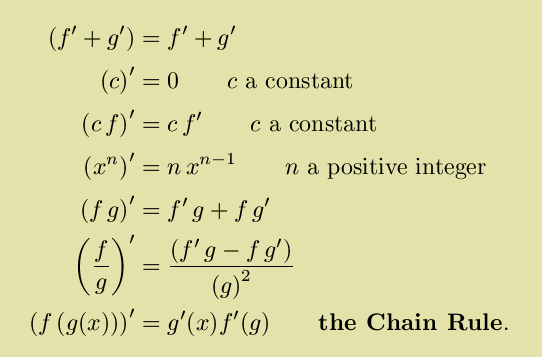
wherever the limit exists. The derivative has many interpretations and applications, including velocity (where f gives position as a function of time), instantaneous rate of change, or slope of a tangent line to the graph of f. Using the algebraic properties of limits, you can prove these extremely important algebraic properties of derivatives:

These rules, for example, allow you to calculate the derivative of any rational (= ratio of two polynomials) function. The chain rule in particular has many applications. For one thing, if you have two inverse functions f and g, that is if f(g(x)) = x, then the chain rule implies that f´(g) = 1/g´(x).

Also, if you have an implicitly defined function between x and y like x² - 2 x y + y² = 1, then you can perform implicit differentation (basically, just taking the derivative of everything with respect to both x and y are tacking on dxs and dys to indicate which) to get 2x dx - 2 x dy - 2 y dx + 2 y dy = 0. Then if you solve for dy/dx, this will be equal (by the chain rule) to y´ and if you solve for dx/dy, this will be equal to x´. Note that in this case, either derivative will be in terms of both x and y.

You may be wondering about the derivatives of your favorite trigonometric functions. Well,

These two facts, combined with the rules above, allow one to calculate easilythe derivatives of the rest of the trigonometric functions and their inverses. The derivatives of the hyperbolic functions are similar, except that

Many physical applications of derivatives reduce to finding solutions to differential equations: equations relating a function and its derivatives. For example, both sine and cosine satisfy the differential equation f´´(x) = -f(x), which models ideal pendulums, springs, and other examples of simple harmonic motion. The equation f´(x) = k f(x) comes up in modeling population growth and radioactive decay, and is solved by the function f(x) = e^kx, where

is called Euler's constant and is defined to be the unique real number e such that (e^x)´ = e^x. The inverse of the exponential function e^x is the natural logarithm function log(x), which has many useful and interesting properties, including:

log(ab) = log a + log b
[This way logarithms turn multiplications into into additions was why log tables (and their analog cousins, slide rules) were used to do long multiplications before computers came along.]
log(a/b) = log a - log b
e^{(log x )} = x and log e^x = x
log x^a = a log x
a^x = e^{(x log a)}
(log(x))´ = 1/x
log 1 = 0 Closely related to the natural logarithm is the logarithm to the base b, (log_b x), which can be defined as log(x)/log(b).
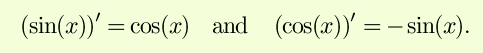
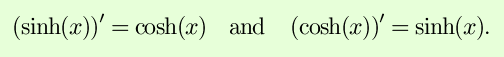
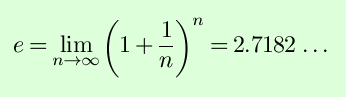
Finally, derivatives can be used to help you graph functions. First, they give you the slope of the graph at a point, which is useful. Second, the points where the slope of the graph is horizontal (f´(x) = 0) are particularly important, because these are the only points at which a relative minimum or maximum can occur (in a differentiable function). These points where f´(x)) = 0 are called critical points. To determine whether a critical point is a minimum or maximum, or more generally to determine the concavity of a function, second derivatives can be used; f´´(x) < 0 means a relative maximum/concave down, f´´(x) > 0 means a relative minimum /concave up. Finally, taking the limit as x goes to positive or negative infinity gives information about the function's asympotitic behavior. Towards that end, derivatives can help you out with some difficult limits: by L'Hôpital's rule, if lim f(x) and lim g(x) are both zero, then lim f(x)/lim g(x) = lim f´(x)/lim g´(x). The proof of L'Hôpital's rule relies on the Mean Value Theorem: that for any function f(x) differentiable between a and b, there is some point c between a and b such that the derivative of f at c is the same as the average slope between a and b:

Integrals
The integral of f(x) from a to b with respect to x is noted as
and gives the area under the graph of f and above the interval [a,b]. It can be defined formally as a Riemann sum: the limit of the areas of rectangular approximations to the area as the approximations get better and better.
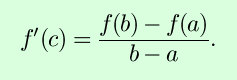
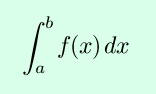
As stated before, integration and differentiation are inverse operations. To be precise, the fundamental theorem of calculus states that
More generally, using an application of the Chain Rule,
Knowing these facts, we now know a tremendous number of integrals: just flip the sides of any table of derivatives. Here are some further facts about integrals:
For c a constant,

The integral of a positive, continuous function from a to b with b > a is greater than zero.
The integral from a to b of f(x)-g(x), with f(x) > g(x) in the interval [a,b] gives the area between f(x) and g(x).
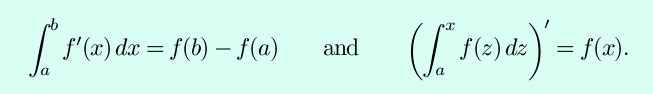
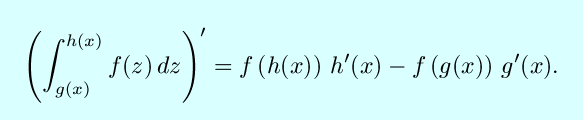
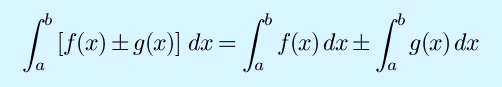
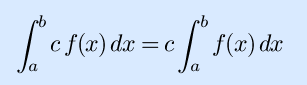
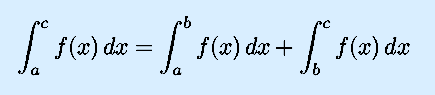
If those properties aren't enough to solve your integral, and if you can't find it in any table, then here are some further tricks of the trade:
- Substitution (the ``inverse'' of the Chain Rule):
- Integration by parts (the ``invserse'' of the Product Rule):
- Partial fractions: Every rational function with a denomminator which can be broken up into the sum of fractions of the form
  where A, B, C, D and E are constants (of course not the same constants in the two forms) may be (more) easily integrated.
- Numerical approximation. This may not give you give you an exact answer, but approximating the area under f(x) with rectangles, trapezoids, or even more complicated shapes can give you a value near the integral when no other method will work. For a brief explanation of the use of an application available to MIT students, see Definite Integrals on Maple, part of Using Maple for ESG Subjects, used as part of the MIT subject 18.01A at ESG.
Integrals are defined to find areas, but they can also be used to calculate other measure properties such as length or volume. For instance, the integral
gives the arclength of the graph of f(x) between x=a and x=b. The integral
gives the volume contained by revolving the graph of f(x) between x=a and x=b about the x-axis. The integral
gives the volume contained by revolving the graph of f(x) between x=a and x=b about the y-axis. Finally, the surface area of the surface formed by revolving the graph of f(x) between x=a and x=b about the x-axis can be found by the integral
Sometimes you will wish to take an integral over an unbounded interval such as from 1 to infinity, or to take an integral of a function that is undefined at some points (such as 1/x^1/2). These are improper integrals, and can be found by taking the limit of an integral over an interval that either grows towards infinity or towards the points where the function is undefined.

Calculus Index Page | Back to the World Web Math Categories Page

watko@mit.edu
Last Modifed January 10, 2000.

Calculus Summary

Derivatives

Integrals