Conceptually Understanding Balance

If you want to learn about balance from a physics perspective, this might be a good place to start. Whether you are a unicyclist, an academic, or an athlete, I think that learning just a bit about physics will help you to balance.

This site presents a simplified fun summary of my senior thesis on conceptually understanding balance. You can read the full version of my thesis here.

Mechanisms of Balance

My thesis starts with the bold statement that there are three mechanisms of balance, and that we can think about each one to help understand how someone balances. The picture below shows these three mechanisms of balance, and we'll talk about the first two in more detail.

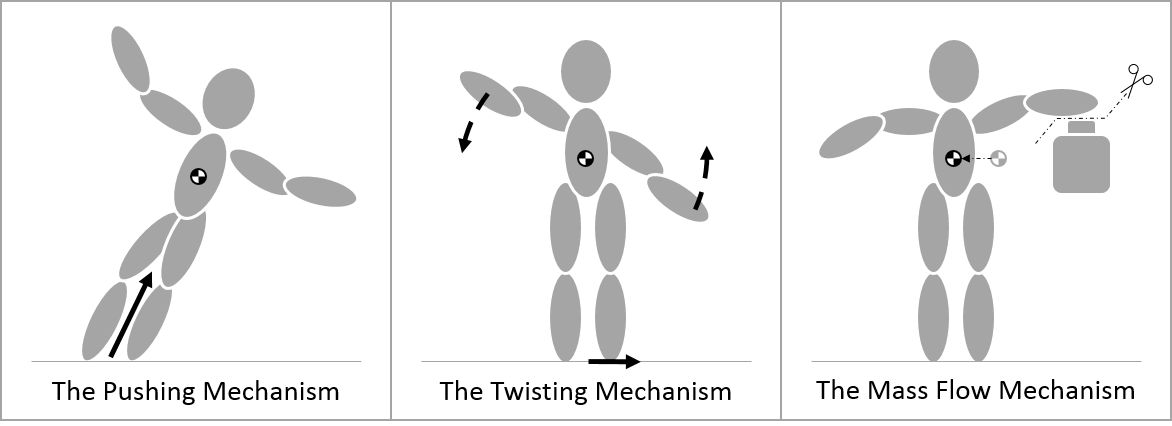
So the above picture shows three mechanisms which are super cool because we can perfectly break down balance into these three mechanisms.

But before I get ahead of myself, let's make sure that you understand what's going on in the picture. First, the center black and white circle is called the center of mass. The center is mass is where we can effectively pretend all the mass of a system is concentrated. This is important, because we can take any system or any collection of objects and then analyze it like its mass is all concentrated at one point. Broadly speaking, we'll be able to use these mechanisms of balance to analyze any Newtonian system big or small.

Now in the pushing and twisting mechanisms you also notice there are forces (the solid black arrows). A force is often defined as simply a push or a pull, and in this case, the forces shown are actually special components of the net contact force or essentially the sum all forces on the system besides the force of gravity.

Deriving the Mechanisms of Balance

The first two mechanisms of balance come directly from a special decomposition of the net contact force. A decomposition for forces is when you take a force and then you split it up into other forces. To appreciate this special decomposition, let's cover:

(a) The traditional decomposition with normal and frictional forces
(b,c) My decomposition with pushing and twisting forces

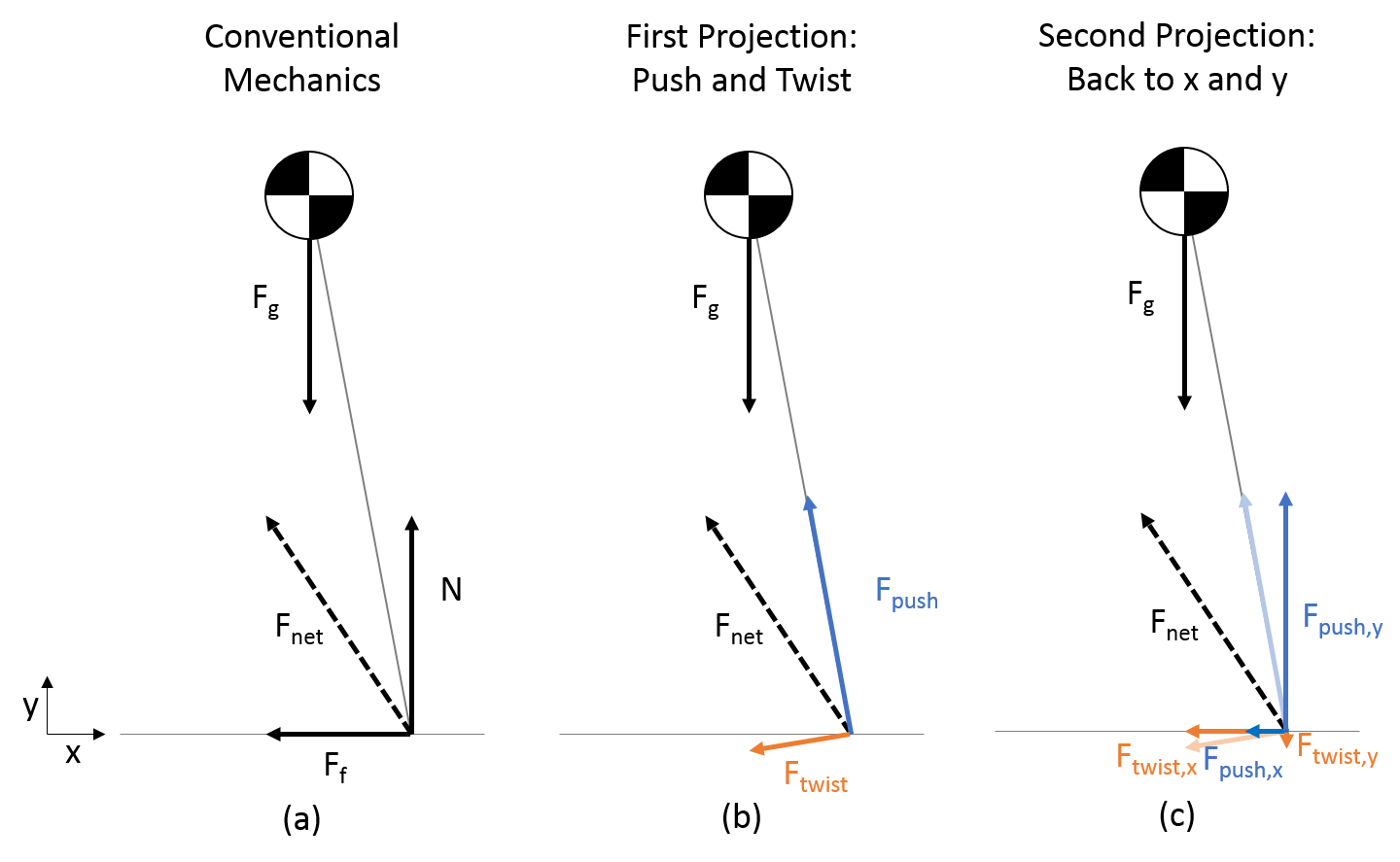
The above picture shows a force with the dashed line that is the net contact force. Your physics teacher might have encouraged you to simply label the net contact force with a normal force N and a friction force F. The normal force would be perpendicular to the surface and then the frictional force is always along the surface. This traditional decomposition is usually good because you can relate the force of friction to the normal force using the coefficient of friction u (with F = u N). However, it's just a decomposition, and we could easily make up a different decomposition.

The decomposition that we will use for this analysis is the center one and then a further decomposition to the right. We take the net contact force and then split this force into two components. One component, the "pushing force," is along the axis from the center of pressure to the center of mass. The other component, "the twisting force," is whatever is perpendicular.

The reason why this unique decomposition is useful is because the "pushing force" helps to accelerate the center of mass closer or away from the center of pressure. And then the "twisting force" is responsible for the changes in rotation of the system about its center of mass. We can say the pushing force is the pushing mechanism and the twisting force (as well as a possible torque not shown) is the twisting mechanism. We can then think about each mechanism separately.

Only the Horizontal Matters

You may have noticed that the above picture actually does another decomposition with the pushing and twisting forces (in c). You could call this a double projection. The pushing and twisting forces are split into their vertical and horizontal components.

The reason why this second projection matters is because in most practice, balance is primarily concerned about horizontal motion. The word "balance" tends to make people think of preventing a fall (vertical motion), but assuming that people can prevent themselves from falling, the largest challenge is then how to move forwards and backwards, left and right.

For instance, although one could try to calculate how people balance on a bicycle to keep from falling, most riders know how to keep from falling. Instead, most riders are focused on how to get from one place to another. And, if we can control one's motion horizontally, we can then keep a rider's center of mass over the center of pressure, and therefore falling and vertical motion is no longer a major concern. In other words, if we understand the horizontal motion, preventing vertical falling is trivial.

The Center of Pressure

Before we describe the first two mechanisms in detail, it is useful to consider the definition for the center of pressure. This definition is important because it changes what is in the twisting mechanism vs. what is in the pushing mechanism. We can just think of the center of pressure as where the force tends to be concentrated along the ground such that we can pretend all the contact force effectively originates. Let's see this through some pictures.

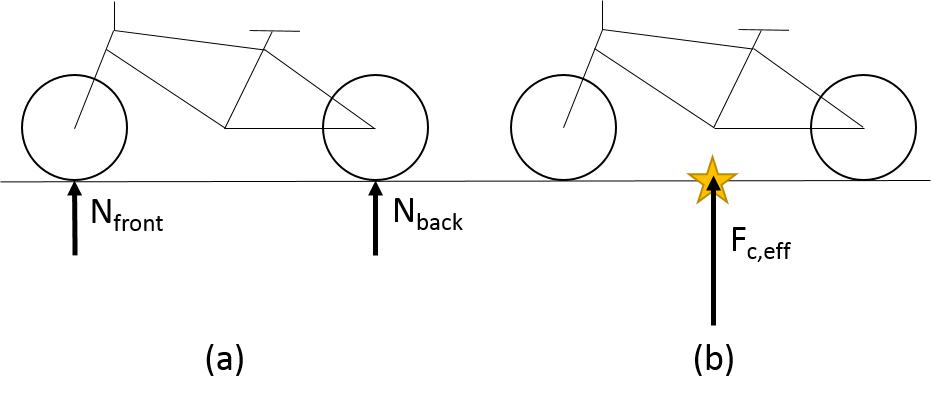
For a bicycle, the center of pressure is going to fall somewhere directly between the wheels. Fairly simply in this case, but note the center of pressure is not necessary where the system directly touches the ground.

For a flag pole with wind the effective center of pressure can actually be away from where the object is touching the ground. This is because the object is connected to the ground in a rigid way and the ground may have to even pull on one side to try to keep the flag pole from falling over. The flag pole example highlights that the center of pressure can be a little unintuitive with complex systems, although usually it's rather straightforward to interpret.

The Pushing Mechanism

So now we are going to focus on the pushing mechanism. I called it the pushing mechanism because it deals with the force directly "pushing" from the center of pressure towards the center of pressure. To understand the pushing mechanism, it is important to understand countersteering - or steering in the opposite direction to initiate moving in the direction you want to go.

The right shows what countersteering looks like.

This video gives a fun 5 minute introduction to countersteering on a unicycle. If you know your physics well, skip to about 1:55.

Three main takeaways from the video are:

The unicycle/unicyclist system has the forces of gravity, the normal force, and the force of friction.
Countersteering is moving the point of contact (aka center of pressure) in the opposite direction to initiate a turn.
Countersteering isn't just for turning left and right, but also moving faster forwards and backwards.

Countersteering is directly related to the pushing force. Steering such that the point of contact is moved out from under the center of mass allows the pushing force to have a significant component horizontally. This results in changes in the horizontal motion.

The Twisting Mechanism

The next question is how do arms help someone to balance. Well, the twisting force is any force in the plane that 1) is perpendicular to the center of pressure to center of mass axis and 2) goes through the "ground." The contact force with the ground is inherently a reaction force meaning that it is a reaction to accelerations and movements of the system. That said, twisting one's arms, bending at the hip, or extending one's leg all can create these lateral forces that go into the twisting force.

Let's have an example. Think of a time where you've almost fallen into a pool and you swung your arms in a giant circle over your head and bowed forward. This was an example of creating a twisting force at your feet backwards that helps to propel your center of mass back.

However, the twisting mechanism is unfortunately limited in magnitude because the arms can only accelerate / move so far. You know that if you lean too far over the edge of a pool, you will fall in. For this reason, the twisting mechanism is often used to initiate leaning and then the pushing force takes over. For this reason, it is possible to turn without steering in the opposite direction, although countersteering will certainly make it more effective.

Additionally, when twisting one's arms, it is useful to have the arms fully extended. This increases the arm's moment of inertia. A larger moment of inertia means that twisting action with the arms results in more feet kick below and thus greater lateral force.

How can I use this?

So now you know:

There are two main mechanisms of balance: the pushing mechanism and the twisting mechanism.
Balance is most concerned with horizontal motion.
The pushing mechanism is highly associated with countersteering which is steering in the opposite direction to initiate a turn.
The twisting mechanism includes actions such as arm swinging, bending at the hip, and extending one's leg.

You can use this knowledge in many ways, but I will give a few examples:

If you have to balance on something you can try to make the most of both of these mechanisms of balance.

On a bicycle, try small countersteering actions that could help you steer in emergency situations better.
On a unicycle, try making extra sharp turns by countersteering hard and extending one's arms while twisting them

When designing something, consider what mechanisms of balance are in use and what limits them.

Say you are designing a new skateboard. Can you allow a sharper turn radius for long distance countersteering while keeping the board stiff enough for small scale countersteering?

If you have a friend who likes balance, please share this with them!

If you are curious about how this applies to airplanes, want to see more of the math, or just generally are interested in this subject, please see the original thesis. Thanks!

Teacher Resources

The short countersteering video content is also available as a TED-Ed lesson with quiz questions and a discussion area. This could make a good short learning activity.

Below is a set of PowerPoint presentations I created and used to teach middle and high school students mechanics in a conceptual approach.
You might be interested in these PPT resources if:

You are a teacher hoping for some cool applications of mechanics
You are a student trying to preview mechanics
You are a unicyclist or other sports fan trying to understand the mechanics behind what you do

These PPT resources are free for you to use, copy, and adapt, with only a few strings attached:

You must absolutely put safety first. Many slides contain the "Physics of Unicycling." Some of these applications of mechanics are dangerous and you must assume all responsibility or have a way of denying any such responsibility for anyone you share this material with.
I would enjoy being credited with this work, but my name/email does not need to be on any of the resources here if there resources are used for general classroom instruction. I would love to hear your comments and I will try to respond to any requests at jabbott(at)mit.edu.
Much care has been taken to only use open-source / creative-commons content. Please respect the use of other material and abide by their policy. Most of their content cannot be commercially sold, but it should be usable for educational creation.

Thank you for exploring these resources. I hope you find them intriguing, interesting, and intellectual!

December 2014