Variance Reduction: Noise reduction with no approximation

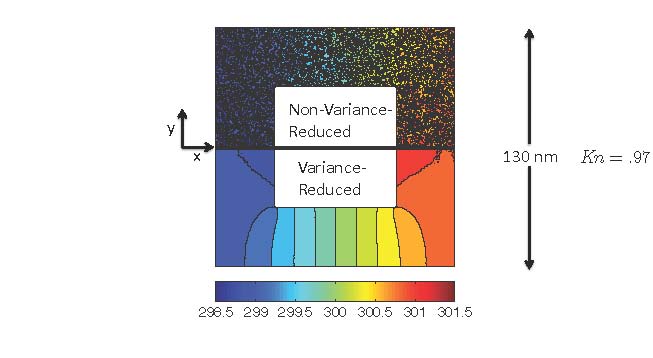
Figure caption: Comparison between a variance-reduced and regular Monte Carlo simulation of phonon transport in porous silicon for the same cost. The achieve the same level of noise, the regular simulation needs to be run 10000 times longer.

Although powerful, Monte Carlo simulations of the Boltzmann transport equation suffer from statistical noise (uncertainty), which can make them prohibitively expensive in the low-signal limit. The statistical uncertainty of such approaches can be drastically reduced using the variance-reduction method of control variates, which in the present context can be applied by simulating only the deviation from equilibrium [1] . In other words, by noting that small signals (e.g. low Mach number, or low temperature differences) result from small deviations from equilibrium, simulating the deviation from equilibrium can be used as a general solution to these limitations, without introducing an approximation.

Deviational methods s imulating only the deviation from equilibrium decompose the non-equilibrium distribution into an equilibrium and a (small) non-equilibrium component, and simulate the corresponding to stochastic particle dynamics the non-equilibrium component. Variance reduction is achieved because the Monte Carlo procedure is used to evaluate only a small part of the solution (the equilibrium part and its moments are known analytically and thus do not contribute to the noise).

Deviational formulations can capture arbitrarily small devations from equilibrium, since as the signal becomes smaller the uncertainty becomes smaller and thus the cost of achieving the same signal-to-noise ratio. In contrast, the cost of regular Monte Carlo grows quadratically for the same signal-to-noise ratio as the signal decreases. The figure above shows a comparison between a deviational and a regular Monte Carlo simulation of phonon transport in porous Silicon.

Related publications:

1. Baker, L.L. and N.G. Hadjiconstantinou, "Variance Reduction for Monte Carlo Solutions of the Boltzmann Equation," Physics of Fluids, 17, 051703, 1-4, 2005. (view)

2. Homolle, T.M.M. and N.G. Hadjiconstantinou, “A Low-variance Deviational Simulation Monte Carlo for the Boltzmann Equation,” Journal of Computational Physics, 226, 2341-2358, 2007. (view)

3. Radtke, G.A. and N.G. Hadjiconstantinou, “Variance-reduced Particle Simulation of the Boltzmann Transport Equation in the Relaxation-time Approximation,” Physical Review E, 79, 056711, 2009. (view)

4. Al-Mohssen, H.A. and N.G. Hadjiconstantinou, “Low-Variance Direct Monte Carlo Simulations Using Importance Weights,” Mathematical Modeling and Numerical Analysis, 44, 1069-1083, 2010. (view)

5. Hadjiconstantinou, N.G., Radtke, G.A. and L.L. Baker, “On Variance Reduced Simulations of the Boltzmann Transport Equation for Small-scale Heat Transfer Applications,” Journal of Heat Transfer, 132, 112401, 2010. (view)

6. Radtke, G.A., Hadjiconstantinou, N.G., and W. Wagner, “Low-Noise Monte Carlo Simulation of the Variable Hard-Sphere Gas,” Physics of Fluids, 23, 030606, 2011 (view )

7. Péraud, J-P.M. and N.G. Hadjiconstantinou, "Efficient simulation of multidimensional phonon transport using energy-based variance-reduced Monte Carlo formulations," Physical Review B, 84, 205331, 2011. (view)

8. Péraud, J-P.M, Landon, C.D. and Hadjiconstantinou, N.G. Monte Carlo Methods for Solving the Boltzmann Transport Equation, Annual Review of Heat Transfer, 17, 205-265, 2014. (view)

9. Landon, C.D. and Hadjiconstantinou, N.G., Deviational Simulation of Phonon Transport in Graphene Ribbons with Ab Initio Scattering, Journal of Applied Physics 116, 163502, 2014. (view)