Nanoscale Gas Transport

Gas transport through nanoporous graphene

Using Molecular Dynamics simulations and kinetic theory arguments we developed a model [1] for describing transport through nanoporous graphene. We subsequently used this model to design and fabricate nanoporous graphene membranes for gas separation by size exclusion (molecular sieving) [2,3,4,5].

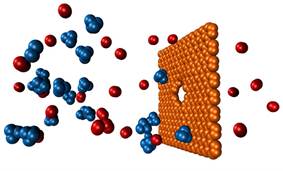
Figure caption: Snapshot of MD simulation of gas separation by a nanoporous graphene membrane

Relevant publications:

1 Sun, C.Z., M. Boutilier, H. Au, P. Poesio, B. Bai, R. Karnik, N.G. Hadjiconstantinou, “Mechanisms of Molecular Permeation through Nanoporous Graphene Membranes,” Langmuir, 30, 675-682, 2014. (view)

2 Boutilier, M.S.H., C.Z. Sun, S.C. O’Hern, H. Au, N.G. Hadjiconstantinou, R. Karnik, “Implications of Permeation Through Intrinsic Defects in Graphene on the Design of Defect-Tolerant Membranes for Gas Separation,” ACS Nano, 8, 841-849, 2014. (view)

3 Boutilier, M.S.H., N.G. Hadjiconstantinou and R. Karnik, “Knudsen Effusion through Polymer-Coated Three-Layer Porous Graphene Membranes,” Nanotechnology, 28, 184004, 2017. (view)

4 Wang, L., M.S.H. Boutilier, P.R. Kidambi, D. Jang, N.G. Hadjiconstantinou and R. Karnik, “Fundamental Transport Mechanisms, Fabrication and Potential Applications of Nanoporous Atomically Thin Membranes,” Nature Nanotechnology, 12, 509-522, 2017.(view)

5 Boutilier, M.S.H., D. Jang, J-C. Idrobo, P. Kidambi, N.G. Hadjiconstantinou and R. Karnik, “Molecular Sieving across Centimeter-Scale Single-Layer Nanoporous Graphene Membranes," ACS Nano, 11, 5726-5736, 2017.(view)

Second-order slip

The Navier-Stokes (NS) description breaks down as characteristic flow lengthscales are on the order of, or smaller than, the molecular mean free path. Breakdown of the NS description is quantified by the Knudsen number (Kn), defined as the ratio of the molecular mean free path to the characteristic flow lengthscale. Asymptotic expansion of the Boltzmann equation in the K_n<<1 limit, shows that while the Navier-Stokes description is valid in the bulk, the inhomogeneity associated with the wall presence requires a kinetic correction, which introduces slip at the walls, as well as a kinetic boundary layer at the wall known as Knudsen layer. Slip conditions and coefficients can be rigorously and uniquely derived as matching conditions between this inner and outer solutions (see Y. Sone, Kinetic Theory and Fluid Dynamics, 2002). Our work has contributed to the determination of some of these coefficients as well as the use of high-order slip-flow theory to solve various problems of practical interest.

Relevant Publications:

1. Hadjiconstantinou, N.G., “Comment on Cercignani’s Second-Order Slip Coefficient,” Physics of Fluids, 15, 2352-2354, 2003. (view)

2. Hadjiconstantinou, N.G., “Validation of a Second-Order Slip Model for Dilute Gas Flows,” Microscale Thermophysical Engineering, 9, 137-153, 2005. (view)

3. Hadjiconstantinou, N.G. and H.A. Al-Mohssen, “A Linearized Kinetic Formulation Including a Second-Order Slip Model for an Impulsive Start Problem at Arbitrary Knudsen Numbers,” Journal of Fluid Mechanics, 533, 47-56, 2005. (view)

4. Hadjiconstantinou, N.G., “Oscillatory Shear-Driven Gas Flows in the Transition and Free-Molecular-Flow Regimes,” Physics of Fluids, 17, 100611, 1-9, 2005. (view)

5. Hadjiconstantinou, N.G., “The Limits of Navier-Stokes Theory and Kinetic Extensions for Describing Small Scale Gaseous Hydrodynamics,” Physics of Fluids, 18, 111301, 1-19, 2006. (view)

6. Radtke G.A., Hadjiconstantinou, N.G., Takata S. and K. Aoki, “On the Second-order Temperature Jump Coefficient of a Dilute Gas,” Journal of Fluid Mechanics, 707, 331-341, 2012. (view)

________________________________________________________________________________

Figure caption: Ballistic layers caused by oscillatory wall temperature variation. Lines denote analytical solution of [2], while symbols denote variance-reduced Monte Carlo simulation of the Boltzmann equation, from [4] with permission.

Response to oscillatory forcing and ballistic Stokes layers

We study the response of a gas layer to variations to the properties (velocity, temperature) of its bounding walls. A case of particular interest is the generalization of the second Stokes problem, in which the wall properties vary sinusoidally. In analogy to the Navier-Stokes limit (Stokes problem), at sufficiently high oscillation frequencies, bounded layers form; in other words, the hydrodynamic response is limited to small regions close to the wall. For Kn>>1, this problem can be described using a ballistic Stokes number (S=ωL/c₀) , where ω is the oscillation frequency, L is the system size and c_0 is the most probable molecular speed (at equilibrium). Analytical solutions [1,3] show that hydrodynamic fields decay proportionally to exp[-(ωδ)^2/3], where δ is the distance from the wall.

Relevant Publications:

1. Hadjiconstantinou, N.G., “Oscillatory Shear-Driven Gas Flows in the Transition and Free-Molecular-Flow Regimes,” Physics of Fluids, 17, 100611, 1-9, 2005. (view)

2. Manela, A. and N.G. Hadjiconstantinou, “On the Motion Induced in a Gas Confined in a Small-scale Gap Due to Instantaneous Heating,” Journal of Fluid Mechanics, 593, 453-462, 2007. (view)

3. Manela, A. and N.G. Hadjiconstantinou, “Gas Motion Induced by Unsteady Boundary Heating in a Small-scale Slab,” Physics of Fluids, 20, 117104, 2008. (view)

4. Hadjiconstantinou, N.G., G.A. Radtke and L.L. Baker, "On Variance-Reduced Simulations of the Boltzmann Transport Equation for Small-Scale Heat Transfer Applications," Journal of Heat Transfer, 132, 112401, 2010. (view)