Variance Reduction as a multiscale tool
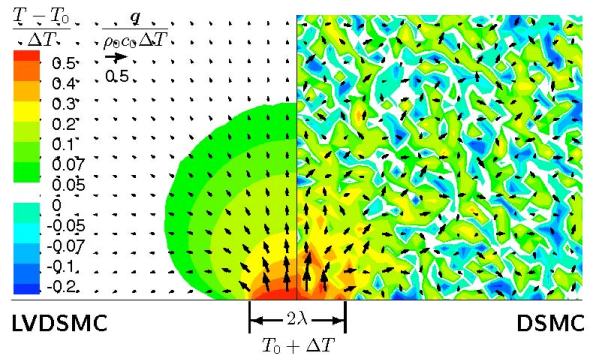
Comparison between a DSMC (Direct Simulation Monte Carlo) and LVDSMC (Low Variance Deviational Simulation Monte Carlo) [1] result for the same computational cost. Produced by G.A. Radtke.
Variance reduction via simulating only the deviation from equilibrium can also be used as a powerful multiscale tool; it separates, in a seamless fashion, the local description into a part that is treated molecularly and a part that can be treated in ways that avoid the large cost associated with the molecular description but retain the same level of fidelity. In other words, the number of particles in the system adjusts dynamically, with regions where little happens described using few particles.
One example is shown in the figure above, whch shows the reponse of a material (gas/semiconducting solid), originally at equilibrium, to a laser pulse. At any instant in time, regions that have not been affected by the pulse remain in equilibrium; in other words, a particle simulation of that region would reproduce the known properties of the equilibrium distribution. Consequently, describing such regions deterministically (using an equilibrium distribution) has two benefits: a) it removes the statistical uncertainty associated with the molecular description (variance reduction); b) it removes the computational cost associated with explicitly simulating the equilibrium regions with particles. Another example is shown in the figure below, where the presence of bounded layers (for more details on bounded layers go here) means that the a large part of the simulation domain is in equilibrium and can thus be described deterministically without using particles [3].
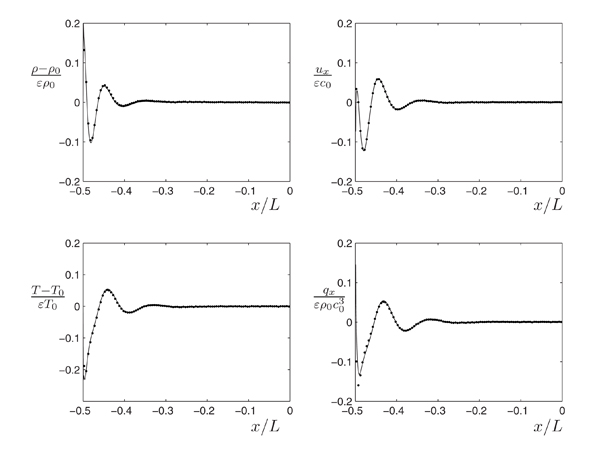
Additionally, as shown in [2], using a spatially variable (local) equilibrium as the control, leads to a particle method which can seamlessly approach the Navier-Stokes limit Kn<<<1 (i.e. simulate large scale problems). This is because as Kn decreases, a local equilibrium description becomes more fitting and, consequently, increasingly larger fraction of the molecular distribution function can be relegated to the deterministic component of the description (the local equilibrium distribution) which is not simulated using particles.
Related Publications:
1. Homolle, T.M.M. and N.G. Hadjiconstantinou, “A Low-variance Deviational Simulation Monte Carlo for the Boltzmann Equation,” Journal of Computational Physics, 226, 2341-2358, 2007. (view)
2. Radtke, G.A. and N.G. Hadjiconstantinou, “Variance-reduced Particle Simulation of the Boltzmann Transport Equation in the Relaxation-time Approximation,” Physical Review E, 79, 056711, 2009. (view)
3. Hadjiconstantinou, N.G., Radtke, G.A., and L.L. Baker, “On Variance-reduced Simulations of the Boltzmann Transport Equation for Small-scale Heat Transfer Applications,” Journal of Heat Transfer, 132, 112401, 2010. (view)
4. Radtke, G.A., Hadjiconstantinou, N.G., and W. Wagner, “Low-Noise Monte Carlo Simulation of the Variable Hard-Sphere Gas,” Physics of Fluids, 23, 030606, 2011. (view)
5. Péraud, J-P.M. and N.G. Hadjiconstantinou, "Efficient simulation of multidimensional phonon transport using energy-based variance-reduced Monte Carlo formulations," Physical Review B, 84, 205331, 2011. (view)

