• Home
• Research
• Microcalorimeters
  • The Basics
  • Transition Edge Sensors
  • Position-Sensitive TES
• Publications
• People
• Job Opportunities
• Our Laboratory
• Links
• Teaching
• Contact Info
• Internal Pages

The Ideal Microcalorimeter

In its most simple incarnation, a microcalorimeter has three parts: an absorber with heat capacity C, a thermometer, and a weak thermal link (with conductance G) to a cold bath at temperature Tb. The cold bath is maintained by a refrigerator at cryogenic temperatures (typically from 50 to 300 milliKelvin depending on the application). When a photon hits the absorber, its energy is converted into heat, which raises the temperature of the absorber. A very sensitive thermometer registers this increase in temperature. The device then cools through the weak thermal link and returns to its quiescent state, ready to detect another photon. The height of the thermal signal is proportional to the energy of the photon. The time constant of this process is determined by the heat capacity C of the absorber and the thermal conductance G of the weak link. The time constant is given by tau=C/G. With these devices we can very accurately determine the energy of the photon, its time of arrival, and by making an array of such devices and placing it at the focal plane of an imaging optic, we can also determine the direction of the photon. Thus we have a single-photon-counting imaging spectrometer.

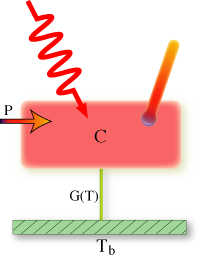
To derive the response of a microcalorimeter to an incident photon, we start by looking at energy flow. The temperature of the absorber will depend on how energy goes in and how much goes out through the weak thermal link:To derive the response of a microcalorimeter to an incident photon, we start by looking at energy flow. The temperature is proportional to the power flowing through the detector:

Where C is the heat capacity of the absorber, T is the temperature of the absorber, P is some power dissipated in the absorber, G is the thermal conductance, Tb is the bath temperature and E is the energy of the photon incident at time t=0.
This equation can be readily solved for the temperature T assuming the Power P is a constant:

So the response to a photon is a single exponential decay from with a time constant τ = C/G and an amplitude proportional to the energy of the photon:


All we need is a good way to accurately measure the temperature of the absorber. In our lab we are developing two different technologies: transition-edge sensors and magnetic calorimeters. Both hold great promise to achieve very high resolutions (E/ΔE > 1000), and we are excited about the possibilities these technologies hold for future large-format detectors for both Earth and Space-borne applications.